graph LR A["📂 Data Pipeline<br><small>Ingestion, Preprocessing, Batching</small>"] -->|Processed<br> Batches| B["⚙️ Training Loop<br><small>Forward Pass, Loss Calculation, Backward Pass</small>"] B -->|Evaluation<br> Metrics| C["📊 Evaluation Pipeline<br><small>Validation and Metrics Computation</small>"] C -->|Feedback| B
8 AI Training
Resources: Slides, Videos, Exercises
Purpose
How do machine learning training workloads manifest as systems challenges, and what architectural principles guide their efficient implementation?
Machine learning training is a unique class of computational workload that demands careful orchestration of computation, memory, and data movement. The process of transforming training algorithms into efficient system implementations requires understanding how mathematical operations map to hardware resources, how data flows through memory hierarchies, and how system architectures influence training performance. Investigating these system-level considerations helps establish core principles for designing and optimizing training infrastructure. By understanding and addressing these challenges, we can develop more efficient and scalable solutions to meet the demands of modern machine learning workloads.
Learning Objectives
Explain the link between mathematical operations and system trade-offs in AI training.
Identify bottlenecks in training systems and their impact on performance.
Outline the key components of training pipelines and their roles in model training.
Determine appropriate optimization techniques to improve training efficiency.
Analyze training systems beyond a single machine, including distributed approaches.
Evaluate and design training processes with a focus on efficiency and scalability.
8.1 Overview
Machine learning has revolutionized modern computing by enabling systems to learn patterns from data, with training being its cornerstone. This computationally intensive process involves adjusting millions—or even billions—of parameters to minimize errors on training examples while ensuring the model generalizes effectively to unseen data. The success of machine learning models hinges on this training phase.
The training process brings together algorithms, data, and computational resources into an integrated workflow. Models, particularly deep neural networks used in domains such as computer vision and natural language processing, require significant computational effort due to their complexity and scale. Even resource-constrained models, such as those used in Mobile ML or Tiny ML applications, require careful tuning to achieve an optimal balance between accuracy, computational efficiency, and generalization.
As models have grown in size and complexity1, the systems that enable efficient training have become increasingly sophisticated. Training systems must coordinate computation across memory hierarchies, manage data movement, and optimize resource utilization—all while maintaining numerical stability and convergence properties. This intersection of mathematical optimization with systems engineering creates unique challenges in maximizing training throughput.
1 Model sizes have grown exponentially since AlexNet (60M parameters) in 2012, with modern large language models like GPT-4 estimated to have over 1 trillion parameters—an increase of over 16,000x in just over a decade.
This chapter examines the key components and architecture of machine learning training systems. We discuss the design of training pipelines, memory and computation systems, data management strategies, and advanced optimization techniques. Additionally, we explore distributed training frameworks and their role in scaling training processes. Real-world examples and case studies are provided to connect theoretical principles to practical implementations, offering insight into the development of efficient, scalable, and effective training systems.
8.2 AI Training Systems
Machine learning training systems represent a distinct class of computational workload with unique demands on hardware and software infrastructure. These systems must efficiently orchestrate repeated computations over large datasets while managing substantial memory requirements and data movement patterns. Unlike traditional high-performance computing workloads, training systems exhibit specific characteristics that influence their design and implementation.
8.2.1 Evolution of Systems
Computing system architectures have evolved through distinct generations, with each new era building upon previous advances while introducing specialized optimizations for emerging application requirements (Figure 8.1). This progression demonstrates how hardware adaptation to application needs shapes modern machine learning systems.
\begin{tikzpicture}[font=\small\sf,node distance=0pt,xscale=2]
\tikzset{
Box/.style={inner xsep=2pt,
draw=black!80, line width=0.75pt,
fill=black!10,
anchor=south,
rounded corners=2pt,
font=\sf\footnotesize,
%text width=27mm,
align=center,
%minimum width=27mm,
minimum height=5mm
},
}
\definecolor{col1}{RGB}{240,240,255}
\definecolor{col2}{RGB}{255, 255, 205}
\def\du{190mm}
\def\vi{15mm}
\node[fill=green!10,draw=none,minimum width=\du,
name path=G4,
anchor=south west, minimum height=\vi](B1)at(-19.0mm,3mm){};
\node[right=2mm of B1.west,anchor=west,align=left]{AI Hypercomputing\\ Era};
\node[fill=col2,draw=none,minimum width=\du,
name path=G3,
anchor=south west, minimum height=\vi](Z)at(B1.north west){};
\node[right=2mm of Z.west,anchor=west,align=left]{Warehouse Scale\\ Computing};
\node[fill=red!10,draw=none,minimum width=\du,
anchor=south west, minimum height=\vi](B2)at (Z.north west){};
\node[right=2mm of B2.west,anchor=west,align=left]{High-Performance\\ Computing};
\node[fill=col1,draw=none,minimum width=\du,
name path=G1,
anchor=south west, minimum height=\vi](V)at(B2.north west){};
\node[right= 2mmof V.west,anchor=west,align=left]{Mainframe};
\def\hi{6.75}
\draw[thick,name path=V1](0mm,0)node[below]{1950}--++(90:\hi);
\draw[thick,name path=V2](10mm,0)node[below]{1960}--++(90:\hi);
\draw[thick,name path=V3](20mm,0)node[below]{1970}--++(90:\hi);
\draw[thick,name path=V4](30mm,0)node[below]{1980}--++(90:\hi);
\draw[thick,name path=V5](40mm,0)node[below]{1990}--++(90:\hi);
\draw[thick,name path=V6](50mm,0)node[below]{2000}--++(90:\hi);
\draw[thick,name path=V7](60mm,0)node[below]{2010}--++(90:\hi);
\draw[thick,name path=V8](70mm,0)node[below]{2020}--++(90:\hi);
\def\fa{2}
\path [name intersections={of=V1 and G1,by={A,B}}];
\node[Box, minimum width=20mm, anchor=south west,
xshift=-\fa*5mm]at([yshift=1pt]B){ENIAC};
\path [name intersections={of=V3 and G1,by={C,D}}];
\node[Box, minimum width=20mm, anchor=north west,
xshift=-\fa*6mm]at([yshift=-1pt]C){IBM\\ System/360};
\node[Box, minimum width=40mm, anchor=north west,
xshift=-\fa*6mm]at([yshift=-1pt]D){CDC 6600};
%%%%
\path [name intersections={of=V4 and G3,by={E,F}}];
\node[Box, minimum width=30mm, anchor=south west,
xshift=-\fa*4mm]at([yshift=1pt]E){Cray-1};
\path [name intersections={of=V6 and G3,by={G,H}}];
\node[Box, minimum width=20mm, anchor=north west,
xshift=0mm]at([yshift=-1pt]G){Google Data\\ Centers};
\path [name intersections={of=V7 and G3,by={I,J}}];
\node[Box, minimum width=22mm, anchor=south west,
xshift=-\fa*5mm]at([yshift=1pt]J){AWS};
\path [name intersections={of=V8 and G4,by={K,L}}];
\node[Box, minimum width=20mm, anchor=north west,
xshift=-\fa*5mm]at([yshift=-1pt]K){NVIDIA GPU};
\node[Box,minimum width=2mm, anchor=south,
xshift=-\fa*0mm]at([yshift=1pt]L){};
\node[minimum width=20mm, anchor=south west,
xshift=-\fa*5mm]at([yshift=1pt]L){Google TPUs};
\end{tikzpicture}Electronic computation began with the mainframe era. ENIAC (1945) established the viability of electronic computation at scale, while the IBM System/360 (1964) introduced architectural principles of standardized instruction sets and memory hierarchies. These fundamental concepts laid the groundwork for all subsequent computing systems.
High-performance computing (HPC) systems (Thornton 1965) built upon these foundations while specializing for scientific computation. The CDC 6600 and later systems like the CM-5 (Corporation 1992) optimized for dense matrix operations and floating-point calculations.
Thornton, James E. 1965. “Design of a Computer: The Control Data 6600.” Communications of the ACM 8 (6): 330–35.
Corporation, Thinking Machines. 1992. CM-5 Technical Summary. Thinking Machines Corporation.
HPC These systems implemented specific architectural features for scientific workloads: high-bandwidth memory systems for array operations, vector processing units for mathematical computations, and specialized interconnects for collective communication patterns. Scientific computing demanded emphasis on numerical precision and stability, with processors and memory systems designed for regular, predictable access patterns. The interconnects supported tightly synchronized parallel execution, enabling efficient collective operations across computing nodes.
Warehouse-scale computing marked the next evolutionary step. Google’s data center implementations (Barroso and Hölzle 2007) introduced new optimizations for internet-scale data processing. Unlike HPC systems focused on tightly coupled scientific calculations, warehouse computing handled loosely coupled tasks with irregular data access patterns.
Barroso, Luiz André, and Urs Hölzle. 2007. “The Case for Energy-Proportional Computing.” Computer 40 (12): 33–37. https://doi.org/10.1109/mc.2007.443.
WSC systems introduced architectural changes to support high throughput for independent tasks, with robust fault tolerance and recovery mechanisms. The storage and memory systems adapted to handle sparse data structures efficiently, moving away from the dense array optimizations of HPC. Resource management systems evolved to support multiple applications sharing the computing infrastructure, contrasting with HPC’s dedicated application execution model.
Deep learning computation emerged as the next frontier, building upon this accumulated architectural knowledge. AlexNet’s (Krizhevsky, Sutskever, and Hinton 2017) success in 2012 highlighted the need for further specialization. While previous systems focused on either scientific calculations or independent data processing tasks, neural network training introduced new computational patterns. The training process required continuous updates to large sets of parameters, with complex data dependencies during model optimization. These workloads demanded new approaches to memory management and inter-device communication that neither HPC nor warehouse computing had fully addressed.
Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. 2017. “ImageNet Classification with Deep Convolutional Neural Networks.” Communications of the ACM 60 (6): 84–90. https://doi.org/10.1145/3065386.
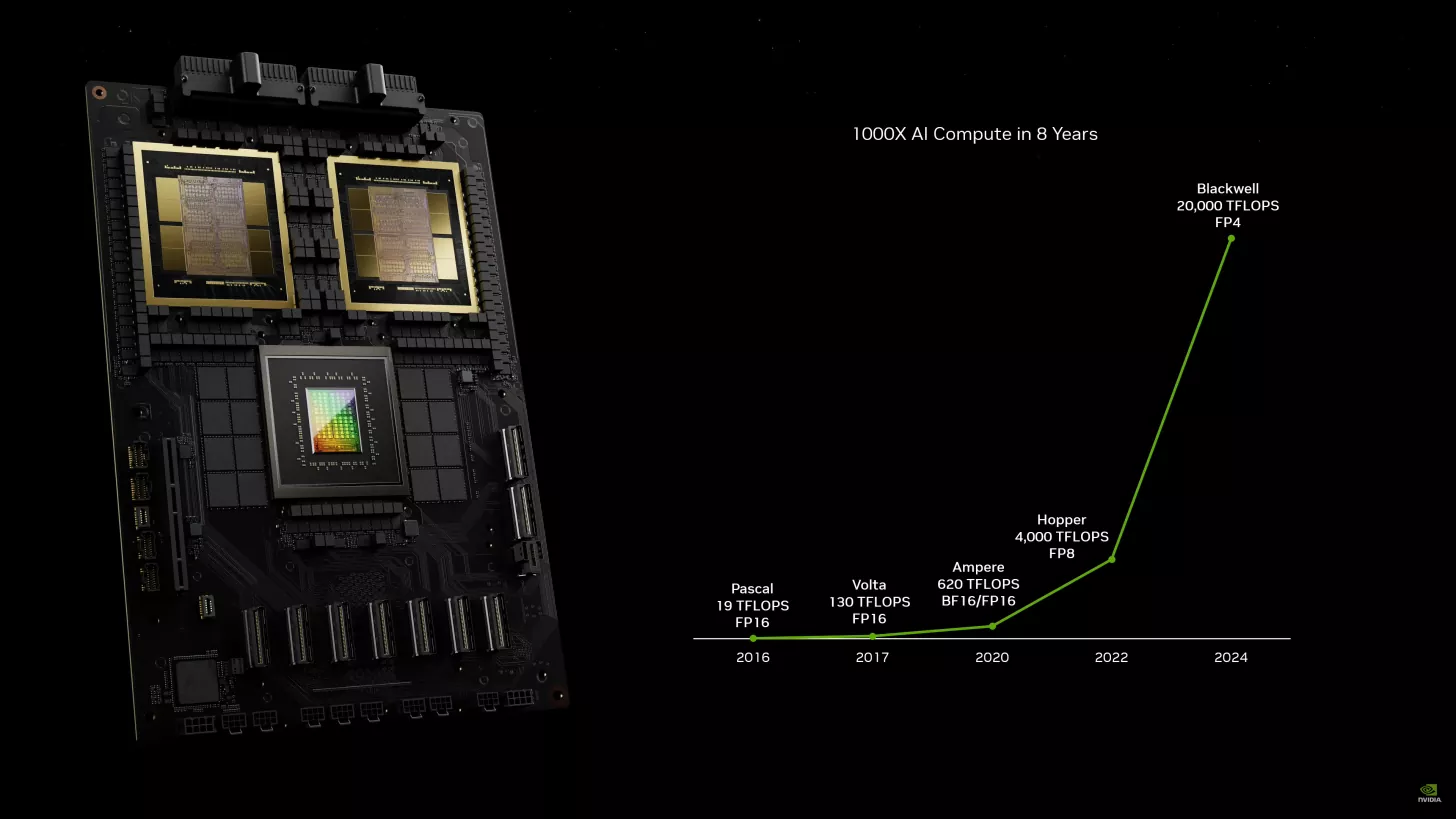
The AI hypercomputing era, beginning in 2015, represents the latest step in this evolutionary chain. NVIDIA GPUs and Google TPUs introduced hardware designs specifically optimized for neural network computations, moving beyond adaptations of existing architectures. These systems implemented new approaches to parallel processing, memory access, and device communication to handle the distinct patterns of model training. The resulting architectures balanced the numerical precision needs of scientific computing with the scale requirements of warehouse systems, while adding specialized support for the iterative nature of neural network optimization.
This architectural progression illuminates why traditional computing systems proved insufficient for neural network training. As shown in Table 8.1, while HPC systems provided the foundation for parallel numerical computation and warehouse-scale systems demonstrated distributed processing at scale, neither fully addressed the computational patterns of model training. Modern neural networks combine intensive parameter updates, complex memory access patterns, and coordinated distributed computation in ways that demanded new architectural approaches.
| Era | Primary Workload | Memory Patterns | Processing Model | System Focus |
|---|---|---|---|---|
| Mainframe | Sequential batch processing | Simple memory hierarchy | Single instruction stream | General-purpose computation |
| HPC | Scientific simulation | Regular array access | Synchronized parallel | Numerical precision, collective operations |
| Warehouse-scale | Internet services | Sparse, irregular access | Independent parallel tasks | Throughput, fault tolerance |
| AI Hypercomputing | Neural network training | Parameter-heavy, mixed access | Hybrid parallel, distributed | Training optimization, model scale |
Understanding these distinct characteristics and their evolution from previous computing eras explains why modern AI training systems require dedicated hardware features and optimized system designs. This historical context provides the foundation for examining machine learning training system architectures in detail.
8.2.2 Role in ML Systems
The development of modern machine learning models relies critically on specialized systems for training and optimization. These systems are a complex interplay of hardware and software components that must efficiently handle massive datasets while maintaining numerical precision and computational stability. While there is no universally accepted definition of training systems due to their rapid evolution and diverse implementations, they share common characteristics and requirements that distinguish them from traditional computing infrastructures.
Definition of Training Systems
Machine Learning Training Systems refer to the specialized computational frameworks that manage and execute the iterative optimization of machine learning models. These systems encompass the software and hardware stack responsible for processing training data, computing gradients, updating model parameters, and coordinating distributed computation. Training systems operate at multiple scales, from single hardware accelerators to distributed clusters, and incorporate components for data management, computation scheduling, memory optimization, and performance monitoring. They serve as the foundational infrastructure that enables the systematic development and refinement of machine learning models through empirical training on data.
These training systems constitute the fundamental infrastructure required for developing predictive models. They execute the mathematical optimization of model parameters, converting input data into computational representations for tasks such as pattern recognition, language understanding, and decision automation. The training process involves systematic iteration over datasets to minimize error functions and achieve optimal model performance.
Training systems function as integral components within the broader machine learning pipeline. They interface with preprocessing frameworks that standardize and transform raw data, while connecting to deployment architectures that enable model serving. The computational efficiency and reliability of training systems directly influence the development cycle, from initial experimentation through model validation to production deployment.
The emergence of transformer architectures and large-scale models has introduced new requirements for training systems. Contemporary implementations must efficiently process petabyte-scale datasets, orchestrate distributed training across multiple accelerators, and optimize memory utilization for models containing billions of parameters. The management of data parallelism, model parallelism, and inter-device communication presents significant technical challenges in modern training architectures.
Training systems also significantly impact the operational considerations of machine learning development. System design must address multiple technical constraints: computational throughput, energy consumption, hardware compatibility, and scalability with increasing model complexity. These factors determine both the technical feasibility and operational viability of machine learning implementations across different scales and applications.
8.2.3 Systems Thinking
The practical execution of training models is deeply tied to system design. Training is not merely a mathematical optimization problem; it is a system-driven process that requires careful orchestration of computing hardware, memory, and data movement.
Training workflows consist of interdependent stages: data preprocessing, forward and backward passes, and parameter updates. Each stage imposes specific demands on system resources. For instance, data preprocessing relies on storage and I/O subsystems to provide computing hardware with continuous input. While traditional processors like CPUs handle many training tasks effectively, increasingly complex models have driven the adoption of hardware accelerators—including Graphics Processing Units (GPUs) and specialized machine learning processors—that can process mathematical operations in parallel. These accelerators, alongside CPUs, handle operations like gradient computation and parameter updates. The performance of these stages depends on how well the system manages bottlenecks such as memory bandwidth and communication latency.
System constraints often dictate the performance limits of training workloads. Modern accelerators are frequently bottlenecked by memory bandwidth, as data movement between memory hierarchies can be slower and more energy-intensive than the computations themselves (Patterson and Hennessy 2021a). In distributed setups, synchronization across devices introduces additional latency, with the performance of interconnects (e.g., NVLink, InfiniBand) playing a crucial role.
Patterson, David A., and John L. Hennessy. 2021a. Computer Architecture: A Quantitative Approach. 6th ed. Morgan Kaufmann.
Optimizing training workflows is essential to overcoming these limitations. Techniques like overlapping computation with data loading, mixed-precision training (Kuchaiev et al. 2018), and efficient memory allocation can significantly enhance performance. These optimizations ensure that accelerators are utilized effectively, minimizing idle time and maximizing throughput.
Beyond training infrastructure, systems thinking has also informed model architecture decisions. System-level constraints often guide the development of new model architectures and training approaches. For example, memory limitations have motivated research into more efficient neural network architectures (M. X. Chen et al. 2018), while communication overhead in distributed systems has influenced the design of optimization algorithms. These adaptations demonstrate how practical system considerations shape the evolution of machine learning approaches within given computational bounds.
Chen, Mia Xu, Orhan Firat, Ankur Bapna, Melvin Johnson, Wolfgang Macherey, George Foster, Llion Jones, et al. 2018. “The Best of Both Worlds: Combining Recent Advances in Neural Machine Translation.” In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), 30:5998–6008. Association for Computational Linguistics. https://doi.org/10.18653/v1/p18-1008.
For example, training large Transformer models requires partitioning data and model parameters across multiple devices. This introduces synchronization challenges, particularly during gradient updates. Communication libraries such as NVIDIA’s Collective Communications Library (NCCL) enable efficient gradient sharing, providing the foundation for more advanced techniques we discuss in later sections. These examples illustrate how system-level considerations influence the feasibility and efficiency of modern training workflows.
8.3 Mathematical Foundations
Neural networks are grounded in mathematical principles that define their structure and functionality. These principles encompass key operations essential for enabling networks to learn complex patterns from data. A thorough understanding of the mathematical foundations underlying these operations is vital, not only for comprehending the mechanics of neural network computation but also for recognizing their broader implications at the system level.
Therefore, we need to connect the theoretical underpinnings of these operations to their practical implementation, examining how modern systems optimize these computations to address critical challenges such as memory management, computational efficiency, and scalability in training deep learning models.
8.3.1 Neural Network Computation
We have previously introduced the basic operations involved in training a neural network (see Chapter 3 and Chapter 4), such as forward propagation and the use of loss functions to evaluate performance. Here, we build on those foundational concepts to explore how these operations are executed at the system level. Key mathematical operations such as matrix multiplications and activation functions underpin the system requirements for training neural networks. Foundational works by Rumelhart, Hinton, and Williams (1986) via the introduction of backpropagation and the development of efficient matrix computation libraries, e.g., BLAS (Dongarra et al. 1988), laid the groundwork for modern training architectures.
Rumelhart, David E., Geoffrey E. Hinton, and Ronald J. Williams. 1986. “Learning Representations by Back-Propagating Errors.” Nature 323 (6088): 533–36. https://doi.org/10.1038/323533a0.
Dongarra, Jack J., Jeremy Du Croz, Sven Hammarling, and Richard J. Hanson. 1988. “An Extended Set of FORTRAN Basic Linear Algebra Subprograms.” ACM Transactions on Mathematical Software 14 (1): 1–17. https://doi.org/10.1145/42288.42291.
Core Operations
At the heart of a neural network is the process of forward propagation, in its simplest case, involves two primary operations: matrix multiplication and the application of an activation function. Matrix multiplication forms the basis of the linear transformation in each layer of the network. At layer \(l\), the computation can be described as: \[ A^{(l)} = f\left(W^{(l)} A^{(l-1)} + b^{(l)}\right) \] Where:
- \(A^{(l-1)}\) represents the activations from the previous layer (or the input layer for the first layer),
- \(W^{(l)}\) is the weight matrix at layer \(l\), which contains the parameters learned by the network,
- \(b^{(l)}\) is the bias vector for layer \(l\),
- \(f(\cdot)\) is the activation function applied element-wise (e.g., ReLU, sigmoid) to introduce non-linearity.
Matrix Operations in Neural Networks
The computational patterns in neural networks revolve around various types of matrix operations. Understanding these operations and their evolution reveals the reasons why specific system designs and optimizations emerged in machine learning training systems.
Dense Matrix-Matrix Multiplication
Matrix-matrix multiplication dominates computation in neural networks, accounting for 60-90% of training time (He et al. 2016). Early neural network implementations relied on standard CPU-based linear algebra libraries. The evolution of matrix multiplication algorithms has closely followed advancements in numerical linear algebra. From Strassen’s algorithm, which reduced the naive \(O(n^3)\) complexity to approximately \(O(n^{2.81})\) (Strassen 1969), to contemporary hardware-accelerated libraries like cuBLAS, these innovations have continually pushed the limits of computational efficiency.
He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. “Deep Residual Learning for Image Recognition.” In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 770–78. IEEE. https://doi.org/10.1109/cvpr.2016.90.
Strassen, Volker. 1969. “Gaussian Elimination Is Not Optimal.” Numerische Mathematik 13 (4): 354–56. https://doi.org/10.1007/bf02165411.
Modern systems implement blocked matrix computations for parallel processing across multiple units. As neural architectures grew in scale, these multiplications began to demand significant memory resources—weight matrices and activation matrices must both remain accessible for the backward pass during training. Hardware designs adapted to optimize for these dense multiplication patterns while managing growing memory requirements.
Matrix-Vector Operations
Matrix-vector multiplication became essential with the introduction of normalization techniques in neural architectures. While computationally simpler than matrix-matrix multiplication, these operations present unique system challenges. They exhibit lower hardware utilization due to their limited parallelization potential. This characteristic influences both hardware design and model architecture decisions, particularly in networks processing sequential inputs or computing layer statistics.
Batched Matrix Operations
The introduction of batching transformed matrix computation in neural networks. By processing multiple inputs simultaneously, training systems convert matrix-vector operations into more efficient matrix-matrix operations. This approach improves hardware utilization but increases memory demands for storing intermediate results. Modern implementations must balance batch sizes against available memory, leading to specific optimizations in memory management and computation scheduling.
Hardware accelerators like Google’s TPU (Jouppi et al. 2017a) reflect this evolution, incorporating specialized matrix units and memory hierarchies for these diverse multiplication patterns. These hardware adaptations enable training of large-scale models like GPT-3 (Brown, Mann, Ryder, Subbiah, Kaplan, and al. 2020) through efficient handling of varied matrix operations.
Brown, Tom B., Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, and et al. 2020. “Language Models Are Few-Shot Learners.” Advances in Neural Information Processing Systems (NeurIPS) 33: 1877–1901.
Activation Functions
Activation functions are central to neural network operation. As shown in Figure 8.2, these functions apply different non-linear transformations to input values, which is essential for enabling neural networks to approximate complex mappings between inputs and outputs. Without activation functions, neural networks, regardless of depth, would collapse into linear systems, severely limiting their representational power (Goodfellow, Courville, and Bengio 2013).
Goodfellow, Ian J., Aaron Courville, and Yoshua Bengio. 2013. “Scaling up Spike-and-Slab Models for Unsupervised Feature Learning.” IEEE Transactions on Pattern Analysis and Machine Intelligence 35 (8): 1902–14. https://doi.org/10.1109/tpami.2012.273.
While activation functions are applied element-wise to the outputs of each neuron, their computational cost is significantly lower than that of matrix multiplications. Typically, activation functions contribute to about 5-10% of the total computation time. However, their impact on the learning process is profound, influencing not only the network’s ability to learn but also its convergence rate and gradient flow.
A careful understanding of activation functions and their computational implications is vital for designing efficient machine learning pipelines. Selecting the appropriate activation function can minimize computation time without compromising the network’s ability to learn complex patterns, ensuring both efficiency and accuracy.
Sigmoid Function
The sigmoid function is one of the original activation functions in neural networks. It maps input values to the range \((0, 1)\) through the following mathematical expression: \[ \text{sigmoid}(x) = \frac{1}{1 + e^{-x}} \]
This function produces an S-shaped curve, where inputs far less than zero approach an output of 0, and inputs much greater than zero approach 1. The smooth transition between these bounds makes sigmoid particularly useful in scenarios where outputs need to be interpreted as probabilities. It is therefore commonly applied in the output layer of networks for binary classification tasks.
The sigmoid function is differentiable and has a well-defined gradient, which makes it suitable for use with gradient-based optimization methods. Its bounded output ensures numerical stability, preventing excessively large activations that might destabilize the training process. However, for inputs with very high magnitudes (positive or negative), the gradient becomes negligible, which can lead to the vanishing gradient problem. This issue is particularly detrimental in deep networks, where gradients must propagate through many layers during training (Hochreiter 1998).
Hochreiter, Sepp. 1998. “The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions.” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 06 (02): 107–16. https://doi.org/10.1142/s0218488598000094.
2 Batch Normalization: A technique that normalizes the input of each layer by adjusting and scaling the activations, reducing internal covariate shift and enabling faster training.
Additionally, sigmoid outputs are not zero-centered, meaning that the function produces only positive values. This lack of symmetry can cause optimization algorithms like stochastic gradient descent (SGD) to exhibit inefficient updates, as gradients may introduce biases that slow convergence. To mitigate these issues, techniques such as batch normalization2 or careful initialization may be employed.
Despite its limitations, sigmoid remains an effective choice in specific contexts. It is often used in the final layer of binary classification models, where its output can be interpreted directly as the probability of a particular class. For example, in a network designed to classify emails as either spam or not spam, the sigmoid function converts the network’s raw score into a probability, making the output more interpretable.
Tanh Function
The hyperbolic tangent, or tanh, is a commonly used activation function in neural networks. It maps input values through a nonlinear transformation into the range \((-1, 1)\). The mathematical definition of the tanh function is: \[ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \]
This function produces an S-shaped curve, similar to the sigmoid function, but with the important distinction that its output is centered around zero. Negative inputs are mapped to values in the range \([-1, 0)\), while positive inputs are mapped to values in the range \((0, 1]\). This zero-centered property makes tanh advantageous for hidden layers, as it reduces bias in weight updates and facilitates faster convergence during optimization (LeCun et al. 1998).
The tanh function is smooth and differentiable, with a gradient that is well-defined for all input values. Its symmetry around zero helps balance the activations of neurons, leading to more stable and efficient learning dynamics. However, for inputs with very large magnitudes (positive or negative), the function saturates, and the gradient approaches zero. This vanishing gradient problem can impede training in deep networks.
The tanh function is often used in the hidden layers of neural networks, particularly for tasks where the input data contains both positive and negative values. Its symmetric range \((-1, 1)\) ensures balanced activations, making it well-suited for applications such as sequence modeling and time series analysis.
For example, tanh is widely used in recurrent neural networks (RNNs), where its bounded and symmetric properties help stabilize learning dynamics over time. While tanh has largely been replaced by ReLU in many modern architectures due to its computational inefficiencies and vanishing gradient issues, it remains a viable choice in scenarios where its range and symmetry are beneficial.
ReLU Function
The Rectified Linear Unit (ReLU) is one of the most widely used activation functions in modern neural networks. Its simplicity and effectiveness have made it the default choice for most machine learning architectures. The ReLU function is defined as: \[ \text{ReLU}(x) = \max(0, x) \]
This function outputs the input value if it is positive and zero otherwise. Unlike sigmoid and tanh, which produce smooth, bounded outputs, ReLU introduces sparsity in the network by setting all negative inputs to zero. This sparsity can help reduce overfitting and improve computation efficiency in many scenarios.
ReLU is particularly effective in avoiding the vanishing gradient problem, as it maintains a constant gradient for positive inputs. However, it introduces another issue known as the dying ReLU problem, where neurons can become permanently inactive if they consistently output zero. This occurs when the weights cause the input to remain in the negative range. In such cases, the neuron no longer contributes to learning.
ReLU is commonly used in the hidden layers of neural networks, particularly in convolutional neural networks (CNNs) and machine learning models for image and speech recognition tasks. Its computational simplicity and ability to prevent vanishing gradients make it ideal for training deep architectures.
Softmax Function
The softmax function is a widely used activation function, primarily applied in the output layer of classification models. It transforms raw scores into a probability distribution, ensuring that the outputs sum to 1. This makes it particularly suitable for multi-class classification tasks, where each output represents the probability of the input belonging to a specific class.
The mathematical definition of the softmax function for a vector of inputs \(\mathbf{z}=[z_1,z_2,\dots,z_K]\) is: \[ \sigma(z_i)=\frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}},\quad i=1,2,\dots,K \] Here, \(K\) is the number of classes, \(z_i\) represents the raw score (logit) for the \(i\)-th class, and \(\sigma(z_i)\) is the probability of the input belonging to that class.
Softmax has several desirable properties that make it essential for classification tasks. It converts arbitrary real-valued inputs into probabilities, with each output value in the range \((0,1)\) and the sum of all outputs equal to 1. The function is differentiable, which allows it to be used with gradient-based optimization methods. Additionally, the probabilistic interpretation of its output is crucial for tasks where confidence levels are needed, such as object detection or language modeling.
However, softmax is sensitive to the magnitude of the input logits. Large differences in logits can lead to highly peaked distributions, where most of the probability mass is concentrated on a single class, potentially leading to overconfidence in predictions.
Softmax finds extensive application in the final layer of neural networks for multi-class classification tasks. For instance, in image classification, models such as AlexNet and ResNet employ softmax in their final layers to assign probabilities to different image categories. Similarly, in natural language processing tasks like language modeling and machine translation, softmax is applied over large vocabularies to predict the next word or token, making it an essential component in understanding and generating human language.
System Trade-offs
Activation functions in neural networks significantly impact both mathematical properties and system-level performance. The selection of an activation function directly influences training time, model scalability, and hardware efficiency through three primary factors: computational cost, gradient behavior, and memory usage.
Benchmarking common activation functions on an Apple M2 single-threaded CPU reveals meaningful performance differences, as illustrated in Figure 8.3. The data demonstrates that Tanh and ReLU execute more efficiently than Sigmoid on CPU architectures, making them particularly suitable for real-time applications and large-scale systems.
While these benchmark results provide valuable insights, they represent CPU-only performance without hardware acceleration. In production environments, modern hardware accelerators like GPUs can substantially alter the relative performance characteristics of activation functions. System architects must therefore consider their specific hardware environment and deployment context when evaluating computational efficiency.
The selection of activation functions requires careful balancing of computational considerations against mathematical properties. Key factors include the function’s ability to mitigate vanishing gradients and introduce beneficial sparsity in neural activations. Each major activation function presents distinct advantages and challenges:
Sigmoid
The sigmoid function has smooth gradients and a bounded output in the range \((0, 1)\), making it useful in probabilistic settings. However, the computation of the sigmoid involves an exponential function, which becomes a key consideration in both software and hardware implementations. In software, this computation is expensive and inefficient, particularly for deep networks or large datasets. Additionally, sigmoid suffers from vanishing gradients, especially for large input values, which can hinder the learning process in deep architectures. Its non-zero-centered output can also slow optimization, requiring more epochs to converge.
These computational challenges are addressed differently in hardware. Modern accelerators like GPUs and TPUs typically avoid direct computation of the exponential function, instead using lookup tables (LUTs) or piece-wise linear approximations to balance accuracy with speed. While these hardware optimizations help, the multiple memory lookups and interpolation calculations still make sigmoid more resource-intensive than simpler functions like ReLU, even on highly parallel architectures.
Tanh
The tanh function outputs values in the range \((-1, 1)\), making it zero-centered and helping to stabilize gradient-based optimization algorithms. This zero-centered output helps reduce biases in weight updates, an advantage over sigmoid. Like sigmoid, however, tanh involves exponential computations that impact both software and hardware implementations. In software, this computational overhead can slow training, particularly when working with large datasets or deep models. While tanh helps prevent some of the saturation issues associated with sigmoid, it still suffers from vanishing gradients for large inputs, especially in deep networks.
In hardware, tanh leverages its mathematical relationship with sigmoid (being essentially a scaled and shifted version) to optimize implementation. Modern hardware often implement tanh using a hybrid approach: lookup tables for common input ranges combined with piece-wise approximations for edge cases. This approach helps balance accuracy with computational efficiency, though tanh remains more resource-intensive than simpler functions. Despite these challenges, tanh remains common in RNNs and LSTMs where balanced gradients are crucial.
ReLU
The ReLU function stands out for its mathematical simplicity: it passes positive values unchanged and sets negative values to zero. This straightforward behavior has profound implications for both software and hardware implementations. In software, ReLU’s simple thresholding operation results in faster computation compared to sigmoid or tanh. It also helps prevent vanishing gradients and introduces beneficial sparsity in activations, as many neurons output zero. However, ReLU can suffer from the “dying ReLU” problem in deep networks, where neurons become permanently inactive and never update their weights.
The hardware implementation of ReLU showcases why it has become the dominant activation function in modern neural networks. Its simple \(\max(0,x)\) operation requires just a single comparison and conditional set, translating to minimal circuit complexity. Modern GPUs and TPUs can implement ReLU using a simple multiplexer that checks the input’s sign bit, allowing for extremely efficient parallel processing. This hardware efficiency, combined with the sparsity it introduces, results in both reduced computation time and lower memory bandwidth requirements.
Softmax
The softmax function transforms raw logits into a probability distribution, ensuring outputs sum to 1, making it essential for classification tasks. Its computation involves exponentiating each input value and normalizing by their sum, a process that becomes increasingly complex with larger output spaces. In software, this creates significant computational overhead for tasks like natural language processing, where vocabulary sizes can reach hundreds of thousands of terms. The function also requires keeping all values in memory during computation, as each output probability depends on the entire input.
At the hardware level, softmax faces unique challenges because it can’t process each value independently like other activation functions. Unlike ReLU’s simple threshold or even sigmoid’s per-value computation, softmax needs access to all values to perform normalization. This becomes particularly demanding in modern transformer architectures, where softmax computations in attention mechanisms process thousands of values simultaneously. To manage these demands, hardware implementations often use approximation techniques or simplified versions of softmax, especially when dealing with large vocabularies or attention mechanisms.
Table 8.2 summarizes the trade-offs of these commonly used activation functions and highlights how these choices affect system performance.
| Function | Key Advantages | Key Disadvantages | System Implications |
|---|---|---|---|
| Sigmoid | Smooth gradients; bounded output in \((0, 1)\). | Vanishing gradients; non-zero-centered output. | Exponential computation adds overhead; limited scalability for deep networks on modern accelerators. |
| Tanh | Zero-centered output in \((-1, 1)\); stabilizes gradients. | Vanishing gradients for large inputs. | More expensive than ReLU; effective for RNNs/LSTMs but less common in CNNs and Transformers. |
| ReLU | Computationally efficient; avoids vanishing gradients; introduces sparsity. | Dying neurons; unbounded output. | Simple operations optimize well on GPUs/TPUs; sparse activations reduce memory and computation needs. |
| Softmax | Converts logits into probabilities; sums to \(1\). | Computationally expensive for large outputs. | High cost for large vocabularies; hierarchical or sampled softmax needed for scalability in NLP tasks. |
The choice of activation function should balance computational considerations with their mathematical properties, such as handling vanishing gradients or introducing sparsity in neural activations. This data emphasizes the importance of evaluating both theoretical and practical performance when designing neural networks. For large-scale networks or real-time applications, ReLU is often the best choice due to its efficiency and scalability. However, for tasks requiring probabilistic outputs, such as classification, softmax remains indispensable despite its computational cost. Ultimately, the ideal activation function depends on the specific task, network architecture, and hardware environment.
8.3.2 Optimization Algorithms
Optimization algorithms play an important role in neural network training by guiding the adjustment of model parameters to minimize a loss function. This process is fundamental to enabling neural networks to learn from data, and it involves finding the optimal set of parameters that yield the best model performance on a given task. Broadly, these algorithms can be divided into two categories: classical methods, which provide the theoretical foundation, and advanced methods, which introduce enhancements for improved performance and efficiency.
These algorithms are responsible for navigating the complex, high-dimensional landscape of the loss function, identifying regions where the function achieves its lowest values. This task is challenging because the loss function surface is rarely smooth or simple, often characterized by local minima, saddle points, and sharp gradients. Effective optimization algorithms are designed to overcome these challenges, ensuring convergence to a solution that generalizes well to unseen data.
The selection and design of optimization algorithms have significant system-level implications, such as computation efficiency, memory requirements, and scalability to large datasets or models. A deeper understanding of these algorithms is essential for addressing the trade-offs between accuracy, speed, and resource usage.
Classical Methods
Modern neural network training relies on variations of gradient descent for parameter optimization. These approaches differ in how they process training data, leading to distinct system-level implications.
Gradient Descent
Gradient descent is the mathematical foundation of neural network training, iteratively adjusting parameters to minimize a loss function. The basic gradient descent algorithm computes the gradient of the loss with respect to each parameter, then updates parameters in the opposite direction of the gradient: \[ \theta_{t+1} = \theta_t - \alpha \nabla L(\theta_t) \]
In training systems, this mathematical operation translates into specific computational patterns. For each iteration, the system must:
- Compute forward pass activations
- Calculate loss value
- Compute gradients through backpropagation
- Update parameters using the gradient values
The computational demands of gradient descent scale with both model size and dataset size. Consider a neural network with \(M\) parameters training on \(N\) examples. Computing gradients requires storing intermediate activations during the forward pass for use in backpropagation. These activations consume memory proportional to the depth of the network and the number of examples being processed.
Traditional gradient descent processes the entire dataset in each iteration. For a training set with 1 million examples, computing gradients requires evaluating and storing results for each example before performing a parameter update. This approach poses significant system challenges: \[ \text{Memory Required} = N \times \text{(Activation Memory + Gradient Memory)} \]
The memory requirements often exceed available hardware resources on modern hardware. A ResNet-50 model processing ImageNet-scale datasets would require hundreds of gigabytes of memory using this approach. Additionally, processing the full dataset before each update creates long iteration times, reducing the rate at which the model can learn from the data.
Stochastic Gradient Descent (SGD)
These system constraints led to the development of variants that better align with hardware capabilities. The key insight was that exact gradient computation, while mathematically appealing, is not necessary for effective learning. This realization opened the door to methods that trade gradient accuracy for improved system efficiency.
These system limitations motivated the development of more efficient optimization approaches. Stochastic gradient descent (SGD) represents a fundamental shift in the optimization strategy. Rather than computing gradients over the entire dataset, SGD estimates gradients using individual training examples: \[ \theta_{t+1} = \theta_t - \alpha \nabla L(\theta_t; x_i, y_i) \] where \((x_i, y_i)\) represents a single training example. This approach drastically reduces memory requirements since only one example’s activations and gradients need storage at any time. The stochastic nature of these updates introduces noise into the optimization process, but this noise often helps escape local minima and reach better solutions.
However, processing single examples creates new system challenges. Modern accelerators achieve peak performance through parallel computation, processing multiple data elements simultaneously. Single-example updates leave most computing resources idle, resulting in poor hardware utilization. The frequent parameter updates also increase memory bandwidth requirements, as weights must be read and written for each example rather than amortizing these operations across multiple examples.
Mini-batch Processing
Mini-batch gradient descent emerges as a practical compromise between full-batch and stochastic methods. It computes gradients over small batches of examples, enabling parallel computations that align well with modern GPU architectures (Dean and Ghemawat 2008). \[ \theta_{t+1} = \theta_t - \alpha \frac{1}{B} \sum_{i=1}^B \nabla L(\theta_t; x_i, y_i) \]
Dean, Jeffrey, and Sanjay Ghemawat. 2008. “MapReduce: Simplified Data Processing on Large Clusters.” Communications of the ACM 51 (1): 107–13. https://doi.org/10.1145/1327452.1327492.
Mini-batch processing aligns well with modern hardware capabilities. Consider a training system using GPU hardware. These devices contain thousands of cores designed for parallel computation. Mini-batch processing allows these cores to simultaneously compute gradients for multiple examples, improving hardware utilization. The batch size B becomes a key system parameter, influencing both computational efficiency and memory requirements.
The relationship between batch size and system performance follows clear patterns. Memory requirements scale linearly with batch size: \[ \text{Memory Required} = B \times \text{(Activation Memory + Gradient Memory)} \]
However, larger batches enable more efficient computation through improved parallelism. This creates a trade-off between memory constraints and computational efficiency. Training systems must select batch sizes that maximize hardware utilization while fitting within available memory.
Advanced Optimization Algorithms
Advanced optimization algorithms introduce mechanisms like momentum and adaptive learning rates to improve convergence. These methods have been instrumental in addressing the inefficiencies of classical approaches (Kingma and Ba 2014).
Kingma, Diederik P., and Jimmy Ba. 2014. “Adam: A Method for Stochastic Optimization.” ICLR, December. http://arxiv.org/abs/1412.6980v9.
Momentum-Based Methods
Momentum methods enhance gradient descent by accumulating a velocity vector across iterations. The momentum update equations introduce an additional term to track the history of parameter updates: \[\begin{gather*} v_{t+1} = \beta v_t + \nabla L(\theta_t) \\ \theta_{t+1} = \theta_t - \alpha v_{t+1} \end{gather*}\] where \(\beta\) is the momentum coefficient, typically set between 0.9 and 0.99. From a systems perspective, momentum introduces additional memory requirements. The training system must maintain a velocity vector with the same dimensionality as the parameter vector, effectively doubling the memory needed for optimization state.
Adaptive Learning Rate Methods
RMSprop modifies the basic gradient descent update by maintaining a moving average of squared gradients for each parameter: \[\begin{gather*} s_t = \gamma s_{t-1} + (1-\gamma)\big(\nabla L(\theta_t)\big)^2 \\ \theta_{t+1} = \theta_t - \alpha \frac{\nabla L(\theta_t)}{\sqrt{s_t + \epsilon}} \end{gather*}\]
This per-parameter adaptation requires storing the moving average \(s_t\), creating memory overhead similar to momentum methods. The element-wise operations in RMSprop also introduce additional computational steps compared to basic gradient descent.
Adam Optimization
Adam combines concepts from both momentum and RMSprop, maintaining two moving averages for each parameter: \[\begin{gather*} m_t = \beta_1 m_{t-1} + (1-\beta_1)\nabla L(\theta_t) \\ v_t = \beta_2 v_{t-1} + (1-\beta_2)\big(\nabla L(\theta_t)\big)^2 \\ \theta_{t+1} = \theta_t - \alpha \frac{m_t}{\sqrt{v_t + \epsilon}} \end{gather*}\]
The system implications of Adam are more substantial than previous methods. The optimizer must store two additional vectors (\(m_t\) and \(v_t\)) for each parameter, tripling the memory required for optimization state. For a model with 100 million parameters using 32-bit floating-point numbers, the additional memory requirement is approximately 800 MB.
System Implications
The practical implementation of both classical and advanced optimization methods requires careful consideration of system resources and hardware capabilities. Understanding these implications helps inform algorithm selection and system design choices.
Trade-offs
The choice of optimization algorithm creates specific patterns of computation and memory access that influence training efficiency. Memory requirements increase progressively from basic gradient descent to more sophisticated methods: \[\begin{gather*} \text{Memory}_{\text{SGD}} = \text{Size}_{\text{params}} \\ \text{Memory}_{\text{Momentum}} = 2 \times \text{Size}_{\text{params}} \\ \text{Memory}_{\text{Adam}} = 3 \times \text{Size}_{\text{params}} \end{gather*}\]
These memory costs must be balanced against convergence benefits. While Adam often requires fewer iterations to reach convergence, its per-iteration memory and computation overhead may impact training speed on memory-constrained systems.
Implementation Considerations
The efficient implementation of optimization algorithms in training frameworks hinges on strategic system-level considerations that directly influence performance. Key factors include memory bandwidth management, operation fusion techniques, and numerical precision optimization. These elements collectively determine the computational efficiency, memory utilization, and scalability of optimizers across diverse hardware architectures.
Memory bandwidth presents the primary bottleneck in optimizer implementation. Modern frameworks address this through operation fusion, which reduces memory access overhead by combining multiple operations into a single kernel. For example, the Adam optimizer’s memory access requirements can grow linearly with parameter size when operations are performed separately: \[ \text{Bandwidth}_{\text{separate}} = 5 \times \text{Size}_{\text{params}} \]
However, fusing these operations into a single computational kernel significantly reduces the bandwidth requirement: \[ \text{Bandwidth}_{\text{fused}} = 2 \times \text{Size}_{\text{params}} \]
These techniques have been effectively demonstrated in systems like cuDNN and other GPU-accelerated frameworks that optimize memory bandwidth usage and operation fusion (Chetlur et al. 2014; Jouppi et al. 2017a).
Chetlur, Sharan, Cliff Woolley, Philippe Vandermersch, Jonathan Cohen, John Tran, Bryan Catanzaro, and Evan Shelhamer. 2014. “cuDNN: Efficient Primitives for Deep Learning.” arXiv Preprint arXiv:1410.0759, October. http://arxiv.org/abs/1410.0759v3.
Memory access patterns also play an important role in determining the efficiency of cache utilization. Sequential access to parameter and optimizer state vectors maximizes cache hit rates and effective memory bandwidth. This principle is evident in hardware such as GPUs and tensor processing units (TPUs), where optimized memory layouts significantly improve performance (Jouppi et al. 2017a).
Numerical precision represents another important tradeoff in implementation. Empirical studies have shown that optimizer states remain stable even when reduced precision formats, such as 16-bit floating-point (FP16), are used. Transitioning from 32-bit to 16-bit formats reduces memory requirements, as illustrated for the Adam optimizer: \[ \text{Memory}_{\text{Adam-FP16}} = \frac{3}{2} \times \text{Size}_{\text{params}} \]
Mixed-precision training has been shown to achieve comparable accuracy while significantly reducing memory consumption and computational overhead (Kuchaiev et al. 2018; Krishnamoorthi 2018).
Kuchaiev, Oleksii, Boris Ginsburg, Igor Gitman, Vitaly Lavrukhin, Carl Case, and Paulius Micikevicius. 2018. “OpenSeq2Seq: Extensible Toolkit for Distributed and Mixed Precision Training of Sequence-to-Sequence Models.” In Proceedings of Workshop for NLP Open Source Software (NLP-OSS), 41–46. Association for Computational Linguistics. https://doi.org/10.18653/v1/w18-2507.
Krishnamoorthi, Raghuraman. 2018. “Quantizing Deep Convolutional Networks for Efficient Inference: A Whitepaper.” arXiv Preprint arXiv:1806.08342, June. http://arxiv.org/abs/1806.08342v1.
Chen, Tianqi, Mu Li, Yutian Li, Min Lin, Naiyan Wang, Minjie Wang, Tianjun Xiao, Bing Xu, Chiyuan Zhang, and Zheng Zhang. 2015. “MXNet: A Flexible and Efficient Machine Learning Library for Heterogeneous Distributed Systems.” arXiv Preprint arXiv:1512.01274, December. http://arxiv.org/abs/1512.01274v1.
The above implementation factors determine the practical performance of optimization algorithms in deep learning systems, emphasizing the importance of tailoring memory, computational, and numerical strategies to the underlying hardware architecture (T. Chen et al. 2015).
Optimizer Trade-offs
The evolution of optimization algorithms in neural network training reveals an important intersection between algorithmic efficiency and system performance. While optimizers were primarily developed to improve model convergence, their implementation significantly impacts memory usage, computational requirements, and hardware utilization.
A deeper examination of popular optimization algorithms reveals their varying impacts on system resources. As shown in Table 8.3, each optimizer presents distinct trade-offs between memory usage, computational patterns, and convergence behavior. SGD maintains minimal memory overhead, requiring storage only for model parameters and current gradients. This lightweight memory footprint comes at the cost of slower convergence and potentially poor hardware utilization due to its sequential update nature.
| Property | SGD | Momentum | RMSprop | Adam |
|---|---|---|---|---|
| Memory Overhead | None | Velocity terms | Squared gradients | Both velocity and squared gradients |
| Memory Cost | \(1\times\) | \(2\times\) | \(2\times\) | \(3\times\) |
| Access Pattern | Sequential | Sequential | Random | Random |
| Operations/Parameter | 2 | 3 | 4 | 5 |
| Hardware Efficiency | Low | Medium | High | Highest |
| Convergence Speed | Slowest | Medium | Fast | Fastest |
Momentum methods introduce additional memory requirements by storing velocity terms for each parameter, doubling the memory footprint compared to SGD. This increased memory cost brings improved convergence through better gradient estimation, while maintaining relatively efficient memory access patterns. The sequential nature of momentum updates allows for effective hardware prefetching and cache utilization.
RMSprop adapts learning rates per parameter by tracking squared gradient statistics. Its memory overhead matches momentum methods, but its computation patterns become more irregular. The algorithm requires additional arithmetic operations for maintaining running averages and computing adaptive learning rates, increasing computational intensity from 3 to 4 operations per parameter.
Adam combines the benefits of momentum and adaptive learning rates, but at the highest system resource cost. Table 8.3 reveals that it maintains both velocity terms and squared gradient statistics, tripling the memory requirements compared to SGD. The algorithm’s computational patterns involve 5 operations per parameter update, though these operations often utilize hardware more effectively due to their regular structure and potential for parallelization.
Training system designers must balance these trade-offs when selecting optimization strategies. Modern hardware architectures influence these decisions. GPUs excel at the parallel computations required by adaptive methods, while memory-constrained systems might favor simpler optimizers. The choice of optimizer affects not only training dynamics but also maximum feasible model size, achievable batch size, hardware utilization efficiency, and overall training time to convergence.
Modern training frameworks continue to evolve, developing techniques like optimizer state sharding, mixed-precision storage, and fused operations to better balance these competing demands. Understanding these system implications helps practitioners make informed decisions about optimization strategies based on their specific hardware constraints and training requirements.
8.3.3 Backpropagation Mechanics
The backpropagation algorithm computes gradients by systematically moving backward through a neural network’s computational graph. While earlier discussions introduced backpropagation’s mathematical principles, implementing this algorithm in training systems requires careful management of memory, computation, and data flow.
Basic Mechanics
During the forward pass, each layer in a neural network performs computations and produces activations. These activations must be stored for use during the backward pass: \[\begin{gather*} z^{(l)} = W^{(l)}a^{(l-1)} + b^{(l)} \\ a^{(l)} = f(z^{(l)}) \end{gather*}\] where \(z^{(l)}\) represents the pre-activation values and \(a^{(l)}\) represents the activations at layer \(l\). The storage of these intermediate values creates specific memory requirements that scale with network depth and batch size.
The backward pass computes gradients by applying the chain rule, starting from the network’s output and moving toward the input: \[\begin{gather*} \frac{\partial L}{\partial z^{(l)}}=\frac{\partial L}{\partial a^{(l)}} \odot f'(z^{(l)}) \\ \frac{\partial L}{\partial W^{(l)}}=\frac{\partial L}{\partial z^{(l)}}\big(a^{(l-1)}\big)^T \end{gather*}\]
Each gradient computation requires access to stored activations from the forward pass, creating a specific pattern of memory access and computation that training systems must manage efficiently.
Backpropagation Mechanics
Neural networks learn by adjusting their parameters to reduce errors. Backpropagation computes how much each parameter contributed to the error by systematically moving backward through the network’s computational graph. This process forms the computational core of the optimization algorithms discussed earlier.
For a network with parameters \(W_i\) at each layer, we need to compute \(\frac{\partial L}{\partial W_i}\)—how much the loss L changes when we adjust each parameter. The computation builds on the core operations covered earlier: matrix multiplications and activation functions, but in reverse order. The chain rule provides a systematic way to organize these computations: \[ \frac{\partial L_{full}}{\partial L_{i}} = \frac{\partial A_{i}}{\partial L_{i}} \frac{\partial L_{i+1}}{\partial A_{i}} ... \frac{\partial A_{n}}{\partial L_{n}} \frac{\partial L_{full}}{\partial A_{n}} \]
This equation reveals key requirements for training systems. Computing gradients for early layers requires information from all later layers, creating specific patterns in data storage and access. These patterns directly influence the efficiency of optimization algorithms like SGD or Adam discussed earlier. Modern training systems use autodifferentiation to handle these computations automatically, but the underlying system requirements remain the same.
Memory Requirements
Training systems must maintain intermediate values (activations) from the forward pass to compute gradients during the backward pass. This requirement compounds the memory demands we saw with optimization algorithms. For each layer l, the system must store:
- Input activations from the forward pass
- Output activations after applying layer operations
- Layer parameters being optimized
- Computed gradients for parameter updates
Consider a batch of training examples passing through a network. The forward pass computes and stores: \[\begin{gather*} z^{(l)} = W^{(l)}a^{(l-1)} + b^{(l)} \\ a^{(l)} = f(z^{(l)}) \end{gather*}\]
Both \(z^{(l)}\) and \(a^{(l)}\) must be cached for the backward pass. This creates a multiplicative effect on memory usage: each layer’s memory requirement is multiplied by the batch size, and the optimizer’s memory overhead (discussed in the previous section) applies to each parameter.
The total memory needed scales with:
- Network depth (number of layers)
- Layer widths (number of parameters per layer)
- Batch size (number of examples processed together)
- Optimizer state (additional memory for algorithms like Adam)
This creates a complex set of trade-offs. Larger batch sizes enable more efficient computation and better gradient estimates for optimization, but require proportionally more memory for storing activations. More sophisticated optimizers like Adam can achieve faster convergence but require additional memory per parameter.
Memory-Computation Trade-offs
Training systems must balance memory usage against computational efficiency. Each forward pass through the network generates a set of activations that must be stored for the backward pass. For a neural network with \(L\) layers, processing a batch of \(B\) examples requires storing: \[ \text{Memory per batch} = B \times \sum_{l=1}^L (s_l + a_l) \] where \(s_l\) represents the size of intermediate computations (like \(z^{(l)}\)) and \(a_l\) represents the activation outputs at layer l.
This memory requirement compounds with the optimizer’s memory needs discussed in the previous section. The total memory consumption of a training system includes both the stored activations and the optimizer state: \[ \text{Total Memory} = \text{Memory per batch} + \text{Memory}_{\text{optimizer}} \]
To manage these substantial memory requirements, training systems use several sophisticated strategies. Gradient checkpointing is a basic approach, strategically recomputing some intermediate values during the backward pass rather than storing them. While this increases computational work, it can significantly reduce memory usage, enabling training of deeper networks or larger batch sizes on memory-constrained hardware (T. Chen et al. 2016).
Chen, Tianqi, Bing Xu, Chiyuan Zhang, and Carlos Guestrin. 2016. “Training Deep Nets with Sublinear Memory Cost.” CoRR abs/1604.06174 (April). http://arxiv.org/abs/1604.06174v2.
Jouppi, Norman P., Cliff Young, Nishant Patil, David Patterson, Gaurav Agrawal, Raminder Bajwa, Sarah Bates, et al. 2017a. “In-Datacenter Performance Analysis of a Tensor Processing Unit.” In Proceedings of the 44th Annual International Symposium on Computer Architecture, 1–12. ACM. https://doi.org/10.1145/3079856.3080246.
The efficiency of these memory management strategies depends heavily on the underlying hardware architecture. GPU systems, with their high computational throughput but limited memory bandwidth, often encounter different bottlenecks than CPU systems. Memory bandwidth limitations on GPUs mean that even when sufficient storage exists, moving data between memory and compute units can become the primary performance constraint (Jouppi et al. 2017a).
These hardware considerations guide the implementation of backpropagation in modern training systems. Specialized memory-efficient algorithms for operations like convolutions compute gradients in tiles or chunks, adapting to available memory bandwidth. Dynamic memory management tracks the lifetime of intermediate values throughout the computation graph, deallocating memory as soon as tensors become unnecessary for subsequent computations (Paszke et al. 2019).
Paszke, Adam, Sam Gross, Francisco Massa, and et al. 2019. “PyTorch: An Imperative Style, High-Performance Deep Learning Library.” Advances in Neural Information Processing Systems (NeurIPS) 32: 8026–37.
8.3.4 System Implications
Efficiently managing the forward pass, backward pass, and parameter updates requires a holistic understanding of how these operations interact with data loading, preprocessing pipelines, and hardware accelerators. For instance, matrix multiplications shape decisions about batch size, data parallelism, and memory allocation, while activation functions influence convergence rates and require careful trade-offs between computational efficiency and learning dynamics.
These operations set the stage for addressing the challenges of training pipeline architecture. From designing workflows for data preprocessing to employing advanced techniques like mixed-precision training, gradient accumulation, and checkpointing, their implications are far-reaching.
8.4 Training Pipeline Architecture
A training pipeline is the framework that governs how raw data is transformed into a trained machine learning model. Within the confines of a single system, it orchestrates the steps necessary for data preparation, computational execution, and model evaluation. The design of such pipelines is critical to ensure that training is both efficient and reproducible, allowing machine learning workflows to operate reliably.
As shown in Figure 8.4, the training pipeline consists of three main components: the data pipeline for ingestion and preprocessing, the training loop that handles model updates, and the evaluation pipeline for assessing performance. These components work together in a coordinated manner, with processed batches flowing from the data pipeline to the training loop, and evaluation metrics providing feedback to guide the training process.
8.4.1 Architectural Overview
The architecture of a training pipeline is organized around three interconnected components: the data pipeline, the training loop, and the evaluation pipeline. These components collectively process raw data, train the model, and assess its performance, ensuring that the training process is efficient and effective.
The data pipeline initiates the process by ingesting raw data and transforming it into a format suitable for the model. This data is passed to the training loop, where the model performs its core computations to learn from the inputs. Periodically, the evaluation pipeline assesses the model’s performance using a separate validation dataset. This modular structure ensures that each stage operates efficiently while contributing to the overall workflow.
Data Pipeline
The data pipeline manages the ingestion, preprocessing, and batching of data for training. Raw data is typically loaded from local storage and transformed dynamically during training to avoid redundancy and enhance diversity. For instance, image datasets may undergo preprocessing steps like normalization, resizing, and augmentation to improve the robustness of the model. These operations are performed in real time to minimize storage overhead and adapt to the specific requirements of the task (LeCun et al. 1998). Once processed, the data is packaged into batches and handed off to the training loop.
LeCun, Yann, Leon Bottou, Genevieve B. Orr, and Klaus -Robert Müller. 1998. “Efficient BackProp.” In Neural Networks: Tricks of the Trade, 1524:9–50. Springer Berlin Heidelberg. https://doi.org/10.1007/3-540-49430-8\_2.
Training Loop
The training loop is the computational core of the pipeline, where the model learns from the input data. Each iteration of the loop involves several key steps:
During the forward pass, the model processes a batch of inputs to produce predictions. This is achieved by passing the data through the layers of the model, where mathematical operations such as matrix multiplications and activations transform the inputs into meaningful outputs.
The predictions are compared to the ground truth labels using a loss function, which quantifies the difference between the predicted and actual values. This loss value serves as a measure of the model’s performance.
In the backward pass, gradients are calculated for each parameter of the model using backpropagation. These gradients indicate how the parameters should be adjusted to reduce the loss. Finally, an optimization algorithm updates the model parameters, completing the training step.
This iterative process continues across multiple batches and epochs, gradually improving the model’s ability to make accurate predictions.
Evaluation Pipeline
The evaluation pipeline provides periodic feedback on the model’s performance during training. Using a separate validation dataset, the model’s predictions are compared against known outcomes to compute metrics such as accuracy or loss. These metrics help to monitor progress and detect issues like overfitting or underfitting. Evaluation is typically performed at regular intervals, such as at the end of each epoch, ensuring that the training process aligns with the desired objectives.
Integration of Components
The data pipeline, training loop, and evaluation pipeline are tightly integrated to ensure a smooth and efficient workflow. Data preparation often overlaps with computation, such as when preprocessing the next batch while the current batch is being processed in the training loop. Similarly, the evaluation pipeline operates in tandem with training, providing insights that inform adjustments to the model or training procedure. This integration minimizes idle time for the system’s resources and ensures that training proceeds without interruptions.
8.4.2 Data Pipeline
The data pipeline moves data from storage to computational devices during training. Like a highway system moving vehicles from neighborhoods to city centers, the data pipeline transports training data through multiple stages to reach computational resources.
flowchart LR
subgraph Storage_Zone[Storage Zone]
Raw_Data[fa:fa-database Raw Data]
end
subgraph CPU_Zone[CPU Preprocessing Zone]
Format[fa:fa-cogs Format]
Process[fa:fa-cogs Process]
Batch[fa:fa-layer-group Batch]
end
subgraph Training_Zone[GPU Training Zone]
GPU1[fa:fa-microchip GPU 1]
GPU2[fa:fa-microchip GPU 2]
GPU3[fa:fa-microchip GPU 3]
end
Raw_Data --> Format
Format --> Process
Process --> Batch
Batch -->|Data| GPU1
Batch -->|Data| GPU2
Batch -->|Data| GPU3
The data pipeline running on the CPU transforms raw data stored on disk into processed batches ready for model training on the GPUs. For an image recognition model, the pipeline reads image files from storage, converts them to the correct format, applies preprocessing operations like resizing and normalization, and delivers them to GPUs for computation. Each stage in this process must work efficiently to maintain a smooth data flow during training, ensuring that the GPUs are consistently fed with data to maximize their utilization and minimize idle time.
Core Components
The performance of machine learning systems is fundamentally constrained by storage access speed, which determines the rate at which training data can be retrieved. This access speed is governed by two primary hardware constraints: disk bandwidth and network bandwidth. The maximum theoretical throughput is determined by the following relationship: \[T_{\text{storage}} =\min(B_{\text{disk}}, B_{\text{network}})\] where \(B_{\text{disk}}\) is the physical disk bandwidth (the rate at which data can be read from storage devices) and \(B_{\text{network}}\) represents the network bandwidth (the rate of data transfer across distributed storage systems). Both quantities are measured in bytes per second.
However, the actual throughput achieved during training operations typically falls below this theoretical maximum due to non-sequential data access patterns. The effective throughput can be expressed as: \[T_{\text{effective}} = T_{\text{storage}} \times F_{\text{access}}\] where \(F_{\text{access}}\) represents the access pattern factor. In typical training scenarios, \(F_{\text{access}}\) approximates 0.1, indicating that effective throughput achieves only 10% of the theoretical maximum. This significant reduction occurs because storage systems are optimized for sequential access patterns rather than the random access patterns common in training procedures.
This relationship between theoretical and effective throughput has important implications for system design and training optimization. Understanding these constraints allows practitioners to make informed decisions about data pipeline architecture and training methodology.
Preprocessing
As the data becomes available, data preprocessing transforms raw input data into a format suitable for model training. This process, traditionally implemented through Extract-Transform-Load (ETL) or Extract-Load-Transform (ELT) pipelines, is a critical determinant of training system performance. The throughput of preprocessing operations can be expressed mathematically as: \[T_{\text{preprocessing}} = \frac{N_{\text{workers}}}{t_{\text{transform}}}\]
This equation captures two key factors:
- \(N_{\text{workers}}\) represents the number of parallel processing threads
- \(t_{\text{transform}}\) represents the time required for each transformation operation
Modern training architectures employ multiple processing threads to ensure preprocessing keeps pace with the consumption rates. This parallel processing approach is essential for maintaining efficient high processor utilization.
The final stage of preprocessing involves transferring the processed data to computational devices (typically GPUs). The overall training throughput is constrained by three factors, expressed as: \[T_{\text{training}} =\min(T_{\text{preprocessing}}, B_{\text{GPU\_transfer}}, B_{\text{GPU\_compute}})\] where:
- \(B_{\text{GPU\_transfer}}\) represents GPU memory bandwidth
- \(B_{\text{GPU\_compute}}\) represents GPU computational throughput
This relationship illustrates a fundamental principle in training system design: the system’s overall performance is limited by its slowest component. Whether preprocessing speed, data transfer rates, or computational capacity, the bottleneck stage determines the effective training throughput of the entire system. Understanding these relationships enables system architects to design balanced training pipelines where preprocessing capacity aligns with computational resources, ensuring optimal resource utilization.
System Implications
The relationship between data pipeline architecture and computational resources fundamentally determines the performance of machine learning training systems. This relationship can be simply expressed through a basic throughput equation: \[T_{\text{system}} =\min(T_{\text{pipeline}}, T_{\text{compute}})\] where \(T_{\text{system}}\) represents the overall system throughput, constrained by both pipeline throughput (\(T_{\text{pipeline}}\)) and computational speed (\(T_{\text{compute}}\)).
To illustrate these constraints, consider image classification systems. The performance dynamics can be analyzed through two critical metrics. The GPU Processing Rate (\(R_{\text{GPU}}\)) represents the maximum number of images a GPU can process per second, determined by model architecture complexity and GPU hardware capabilities. The Pipeline Delivery Rate (\(R_{\text{pipeline}}\)) is the rate at which the data pipeline can deliver preprocessed images to the GPU.
In this case, at a high level, the system’s effective training speed is governed by the lower of these two rates. When \(R_{\text{pipeline}}\) is less than \(R_{\text{GPU}}\), the system experiences underutilization of GPU resources. The degree of GPU utilization can be expressed as: \[\text{GPU Utilization} = \frac{R_{\text{pipeline}}}{R_{\text{GPU}}} \times 100\%\]
Let us consider an example. A ResNet-50 model implemented on modern GPU hardware might achieve a processing rate of 1000 images per second. However, if the data pipeline can only deliver 200 images per second, the GPU utilization would be merely 20%, meaning the GPU remains idle 80% of the time. This results in significantly reduced training efficiency. Importantly, this inefficiency persists even with more powerful GPU hardware, as the pipeline throughput becomes the limiting factor in system performance. This demonstrates why balanced system design, where pipeline and computational capabilities are well-matched, is crucial for optimal training performance.
Data Flows
Machine learning systems manage complex data flows through multiple memory tiers while coordinating pipeline operations. The interplay between memory bandwidth constraints and pipeline execution directly impacts training performance. The maximum data transfer rate through the memory hierarchy is bounded by: \[T_{\text{memory}} =\min(B_{\text{storage}}, B_{\text{system}}, B_{\text{accelerator}})\] Where bandwidth varies significantly across tiers:
- Storage (\(B_{\text{storage}}\)): NVMe storage devices provide 1-2 GB/s
- System (\(B_{\text{system}}\)): Main memory transfers data at 50-100 GB/s
- Accelerator (\(B_{\text{accelerator}}\)): GPU memory achieves 900 GB/s or higher
These order-of-magnitude differences create distinct performance characteristics that must be carefully managed. The total time required for each training iteration comprises multiple pipelined operations: \[t_{\text{iteration}} =\max(t_{\text{fetch}}, t_{\text{process}}, t_{\text{transfer}})\]
This equation captures three components: storage read time (\(t_{\text{fetch?}}\)), preprocessing time (\(t_{\text{process}}\)), and accelerator transfer time (\(t_{\text{transfer}}\)).
Modern training architectures optimize performance by overlapping these operations. When one batch undergoes preprocessing, the system simultaneously fetches the next batch from storage while transferring the previously processed batch to accelerator memory.
This coordinated movement requires precise management of system resources, particularly memory buffers and processing units. The memory hierarchy must account for bandwidth disparities while maintaining continuous data flow. Effective pipelining minimizes idle time and maximizes resource utilization through careful buffer sizing and memory allocation strategies. The successful orchestration of these components enables efficient training across the memory hierarchy while managing the inherent bandwidth constraints of each tier.
Practical Architectures
The ImageNet dataset serves as a canonical example for understanding data pipeline requirements in modern machine learning systems. This analysis examines system performance characteristics when training vision models on large-scale image datasets.
Storage performance in practical systems follows a defined relationship between theoretical and practical throughput: \[T_{\text{practical}} = 0.5 \times B_{\text{theoretical}}\]
To illustrate this relationship, consider an NVMe storage device with 3GB/s theoretical bandwidth. Such a device achieves approximately 1.5GB/s sustained read performance. However, the random access patterns required for training data shuffling further reduce this effective bandwidth by 90%. System designers must account for this reduction through careful memory buffer design.
The total memory requirements for the system scale with batch size according to the following relationship: \[M_{\text{required}} = (B_{\text{prefetch}} + B_{\text{processing}} + B_{\text{transfer}}) \times S_{\text{batch}}\]
In this equation, \(B_{\text{prefetch}}\) represents memory allocated for data prefetching, \(B_{\text{processing}}\) represents memory required for active preprocessing operations, \(B_{\text{transfer}}\) represents memory allocated for accelerator transfers, and \(S_{\text{batch}}\) represents the training batch size.
Preprocessing operations introduce additional computational requirements. Common operations such as image resizing, augmentation, and normalization consume CPU resources. These preprocessing operations must satisfy a fundamental time constraint: \[t_{\text{preprocessing}} < t_{\text{GPU\_compute}}\]
This inequality plays a crucial role in determining system efficiency. When preprocessing time exceeds GPU computation time, accelerator utilization decreases proportionally. The relationship between preprocessing and computation time thus establishes fundamental efficiency limits in training system design.
8.4.3 Forward Pass
The forward pass is the phase where input data propagates through the model, layer by layer, to generate predictions. Each layer performs mathematical operations such as matrix multiplications and activations, progressively transforming the data into meaningful outputs. While the conceptual flow of the forward pass is straightforward, it poses several system-level challenges that are critical for efficient execution.
Compute Operations
The forward pass in deep neural networks orchestrates a diverse set of computational patterns, each optimized for specific neural network operations. Understanding these patterns and their efficient implementation is fundamental to machine learning system design.
At their core, neural networks rely heavily on matrix multiplications, particularly in fully connected layers. The basic transformation follows the form: \[ z^{(l)} = W^{(l)}a^{(l-1)} + b^{(l)} \]
Here, \(W^{(l)}\) represents the weight matrix, \(a^{(l-1)}\) contains activations from the previous layer, and \(b^{(l)}\) is the bias vector. For a layer with \(N\) neurons in the current layer and \(M\) neurons in the previous layer, processing a batch of \(B\) samples requires \(N \times M \times B\) floating-point operations. A typical layer with dimensions of \(512\times1024\) processing a batch of 64 samples executes over 33 million operations.
Modern neural architectures extend beyond these basic matrix operations to include specialized computational patterns. Convolutional networks, for instance, perform systematic kernel operations across input tensors. Consider a typical input tensor of dimensions \(64 \times 224 \times 224 \times 3\) (batch size \(\times\) height \(\times\) width \(\times\) channels) processed by \(7 \times 7\) kernels. Each position requires 147 multiply-accumulate operations, and with 64 filters operating across \(218 \times 218\) spatial dimensions, the computational demands become substantial.
Transformer architectures introduce attention mechanisms, which compute similarity scores between sequences. These operations combine matrix multiplications with softmax normalization, requiring efficient broadcasting and reduction operations across varying sequence lengths. The computational pattern here differs significantly from convolutions, demanding flexible execution strategies from hardware accelerators.
Throughout these networks, element-wise operations play a crucial supporting role. Activation functions like ReLU and sigmoid transform values independently. While conceptually simple, these operations can become bottlenecked by memory bandwidth rather than computational capacity, as they perform relatively few calculations per memory access. Batch normalization presents similar challenges, computing statistics and normalizing values across batch dimensions while creating synchronization points in the computation pipeline.
Modern hardware accelerators, particularly GPUs, optimize these diverse computations through massive parallelization. However, achieving peak performance requires careful attention to hardware architecture. GPUs process data in fixed-size blocks of threads called warps (in NVIDIA architectures) or wavefronts (in AMD architectures). Peak efficiency occurs when matrix dimensions align with these hardware-specific sizes. For instance, NVIDIA GPUs typically achieve optimal performance when processing matrices aligned to \(32\times32\) dimensions.
Libraries like cuDNN address these challenges by providing optimized implementations for each operation type. These systems dynamically select algorithms based on input dimensions, hardware capabilities, and memory constraints. The selection process balances computational efficiency with memory usage, often requiring empirical measurement to determine optimal configurations for specific hardware setups.
The relationship between batch size and hardware utilization illuminates these trade-offs. When batch size decreases from 32 to 16, GPU utilization often drops due to incomplete warp occupation. While larger batch sizes improve hardware utilization, memory constraints in modern architectures may necessitate smaller batches, creating a fundamental tension between computational efficiency and memory usage. This balance exemplifies a central challenge in machine learning systems: maximizing computational throughput within hardware resource constraints.
Memory Management
Memory management is a critical challenge in general, but it is particularly crucial during the forward pass when intermediate activations must be stored for subsequent backward propagation. The total memory footprint grows with both network depth and batch size, following a basic relationship. \[ \text{Total Memory} \sim B \times \sum_{l=1}^{L} A_l \] where \(B\) represents the batch size, \(L\) is the number of layers, and \(A_l\) represents the activation size at layer \(l\). This simple equation masks considerable complexity in practice.
Consider ResNet-50 processing images at \(224\times224\) resolution with a batch size of 32. The initial convolutional layer produces activation maps of dimension \(112\times112\times64\). Using single-precision floating-point format (4 bytes per value), this single layer’s activation storage requires approximately 98 MB. As the network progresses through its 50 layers, the dimensions of these activation maps change—typically decreasing spatially while increasing in channel depth—creating a cumulative memory demand that can reach several gigabytes.
Modern GPUs typically provide between 16 and 24 GB of memory, which must accommodate not just these activations but also model parameters, gradients, and optimization states. This constraint has motivated several memory management strategies:
Activation checkpointing trades computational cost for memory efficiency by strategically discarding and recomputing activations during the backward pass. Rather than storing all intermediate values, the system maintains checkpoints at selected layers. During backpropagation, it regenerates necessary activations from these checkpoints. While this approach can reduce memory usage by 50% or more, it typically increases computation time by 20-30%.
Mixed precision training offers another approach to memory efficiency. By storing activations in half-precision (FP16) format instead of single-precision (FP32), memory requirements are immediately halved. Modern hardware architectures provide specialized support for these reduced-precision operations, often maintaining computational throughput while saving memory.
The relationship between batch size and memory usage creates practical trade-offs in training regimes. While larger batch sizes can improve computational efficiency, they proportionally increase memory demands. A machine learning practitioner might start with large batch sizes during initial development on smaller networks, then adjust downward when scaling to deeper architectures or when working with memory-constrained hardware.
This memory management challenge becomes particularly acute in state-of-the-art models. Recent transformer architectures can require tens of gigabytes just for activations, necessitating sophisticated memory management strategies or distributed training approaches. Understanding these memory constraints and management strategies proves essential for designing and deploying machine learning systems effectively.
8.4.4 Backward Pass
Compute Operations
The backward pass involves processing parameter gradients in reverse order through the network’s layers. Computing these gradients requires matrix operations that demand significant memory and processing power.
Neural networks store activation values from each layer during the forward pass. Computing gradients combines these stored activations with gradient signals to generate weight updates. This design requires twice the memory compared to forward computation. Consider the gradient computation for a layer’s weights: \[ \frac{\partial L}{\partial W^{(l)}} = \delta^{(l)} \cdot \left(a^{(l-1)}\right)^T \]
The gradient signals \(\delta^{(l)}\) at layer \(l\) multiply with transposed activations \(a^{(l-1)}\) from layer \(l-1\). This matrix multiplication forms the primary computational load. For example, in a layer with 1000 input features and 100 output features, computing gradients requires multiplying matrices of size 100 \(\times\) batch_size and batch_size \(\times\) 1000, resulting in millions of floating-point operations.
Memory Operations
The backward pass moves large amounts of data between memory and compute units. Each time a layer computes gradients, it orchestrates a sequence of memory operations. The GPU first loads stored activations from memory, then reads incoming gradient signals, and finally writes the computed gradients back to memory.
To understand the scale of these memory transfers, consider a convolutional layer processing a batch of 64 images. Each image measures \(224\times 224\) pixels with 3 color channels. The activation maps alone occupy 0.38 GB of memory, storing 64 copies of the input images. The gradient signals expand this memory usage significantly - they require 8.1 GB to hold gradients for each of the layer’s 64 filters. Even the weight gradients, which only store updates for the convolutional kernels, need 0.037 GB3.
Memory calculations:
- – Activation maps:
- 64 × 224 × 224 × 3 × 4 bytes = 0.38 GB
- – Gradient signals:
- 64 × 224 × 224 × 64 × 4 bytes = 8.1 GB
- – Weight gradients:
- 7 × 7 × 3 × 64 × 4 bytes = 0.037 GB
Moreover, the backward pass in neural networks require coordinated data movement through a hierarchical memory system. During backpropagation, each computation requires specific activation values from the forward pass, creating a pattern of data movement between memory levels. This movement pattern shapes the performance characteristics of neural network training.
These backward pass computations operate across a memory hierarchy that balances speed and capacity requirements. When computing gradients, the processor must retrieve activation values stored in high-bandwidth memory (HBM) or system memory, transfer them to fast static RAM (SRAM) for computation, and write results back to larger storage. Each gradient calculation triggers this sequence of memory transfers, making memory access patterns a key factor in backward pass performance. The frequent transitions between memory levels introduce latency that accumulates across the backward pass computation chain.
Real-World Training Considerations
Consider training a ResNet-50 model on the ImageNet dataset with a batch of 64 images. The first convolutional layer applies 64 filters of size \(7 \times 7\) to RGB images sized \(224\times 224\). During the backward pass, this single layer’s computation requires: \[ \text{Memory per image} = 224 \times 224 \times 64 \times 4 \text{ bytes} \]
The total memory requirement multiplies by the batch size of 64, reaching approximately 3.2 GB just for storing gradients. When we add memory for activations, weight updates, and intermediate computations, a single layer approaches the memory limits of many GPUs.
Deeper in the network, layers with more filters demand even greater resources. A mid-network convolutional layer might use 256 filters, quadrupling the memory and computation requirements. The backward pass must manage these resources while maintaining efficient computation. Each layer’s computation can only begin after receiving gradient signals from the subsequent layer, creating a strict sequential dependency in memory usage and computation patterns.
This dependency means the GPU must maintain a large working set of memory throughout the backward pass. As gradients flow backward through the network, each layer temporarily requires peak memory usage during its computation phase. The system cannot release this memory until the layer completes its gradient calculations and passes the results to the previous layer.
8.4.5 Parameter Updates and Optimizers
The process of updating model parameters is a fundamental operation in machine learning systems. During training, after gradients are computed in the backward pass, the system must allocate and manage memory for both the parameters and their gradients, then perform the update computations. The choice of optimizer determines not only the mathematical update rule, but also the system resources required for training.
Consider the parameter update process in a machine learning framework:
loss.backward() # Compute gradients
optimizer.step() # Update parametersThese operations initiate a sequence of memory accesses and computations. The system must load parameters from memory, compute updates using the stored gradients, and write the modified parameters back to memory. Different optimizers vary in their memory requirements and computational patterns, directly affecting system performance and resource utilization.
Memory Requirements
Gradient descent, the most basic optimization algorithm that we discussed earlier, illustrates the fundamental memory and computation patterns in parameter updates. From a systems perspective, each parameter update must:
- Read the current parameter value from memory
- Access the computed gradient from memory
- Perform the multiplication and subtraction operations
- Write the new parameter value back to memory
Because gradient descent only requires memory for storing parameters and gradients, it has relatively low memory overhead compared to more complex optimizers. However, more advanced optimizers introduce additional memory requirements and computational complexity. For example, as we discussed previously, Adam maintains two extra vectors for each parameter: one for the first moment (the moving average of gradients) and one for the second moment (the moving average of squared gradients). This triples the memory usage but can lead to faster convergence. Consider the situation where there are 100,000 parameters, and each gradient requires 4 bytes (32 bits):
- Gradient Descent: 100,000 \(\times\) 4 bytes = 400,000 bytes = 0.4 MB
- Adam: 3 \(\times\) 100,000 \(\times\) 4 bytes = 1,200,000 bytes = 1.2 MB
This problem becomes especially apparent for billion parameter models, as model sizes (without counting optimizer states and gradients) alone can already take up significant portions of GPU memory. As one way of solving this problem, the authors of GaLoRE tackle this by compressing optimizer state and gradients and computing updates in this compressed space (Zhao et al. 2024), greatly reducing memory footprint as shown below in Figure 8.6.
Zhao, Jiawei, Zhenyu Zhang, Beidi Chen, Zhangyang Wang, Anima Anandkumar, and Yuandong Tian. 2024. “GaLore: Memory-Efficient LLM Training by Gradient Low-Rank Projection,” March. http://arxiv.org/abs/2403.03507v2.
Computational Load
The computational cost of parameter updates also depends on the optimizer’s complexity. For gradient descent, each update involves simple gradient calculation and application. More sophisticated optimizers like Adam require additional calculations, such as computing running averages of gradients and their squares. This increases the computational load per parameter update.
The efficiency of these computations on modern hardware like GPUs and TPUs depends on how well the optimizer’s operations can be parallelized. While matrix operations in Adam may be efficiently handled by these accelerators, some operations in complex optimizers might not parallelize well, potentially leading to hardware underutilization.
In summary, the choice of optimizer directly impacts both system memory requirements and computational load. More sophisticated optimizers often trade increased memory usage and computational complexity for potentially faster convergence, presenting important considerations for system design and resource allocation in ML systems.
Batch Size and Parameter Updates
Batch size, a critical hyperparameter in machine learning systems, significantly influences the parameter update process, memory usage, and hardware efficiency. It determines the number of training examples processed in a single iteration before the model parameters are updated.
Larger batch sizes generally provide more accurate gradient estimates, potentially leading to faster convergence and more stable parameter updates. However, they also increase memory demands proportionally: \[ \text{Memory for Batch} = \text{Batch Size} \times \text{Size of One Training Example} \]
This increase in memory usage directly affects the parameter update process, as it determines how much data is available for computing gradients in each iteration.
Larger batches tend to improve hardware utilization, particularly on GPUs and TPUs optimized for parallel processing. This can lead to more efficient parameter updates and faster training times, provided sufficient memory is available.
However, there’s a trade-off to consider. While larger batches can improve computational efficiency by allowing more parallel computations during gradient calculation and parameter updates, they also require more memory. On systems with limited memory, this might necessitate reducing the batch size, potentially slowing down training or leading to less stable parameter updates.
The choice of batch size interacts with various aspects of the optimization process. For instance, it affects the frequency of parameter updates: larger batches result in less frequent but potentially more impactful updates. Additionally, batch size influences the behavior of adaptive optimization algorithms, which may need to be tuned differently depending on the batch size. In distributed training, which we discuss later, batch size often determines the degree of data parallelism, impacting how gradient computations and parameter updates are distributed across devices.
Determining the optimal batch size involves balancing these factors within hardware constraints. It often requires experimentation to find the sweet spot that maximizes both learning efficiency and hardware utilization while ensuring effective parameter updates.
8.5 Training Pipeline Optimizations
Efficient training of machine learning models is constrained by bottlenecks in data transfer, computation, and memory usage. These limitations manifest in specific ways: data transfer delays occur when loading training batches from disk to GPU memory, computational bottlenecks arise during matrix operations in forward and backward passes, and memory constraints emerge when storing large intermediate values like activation maps.
These bottlenecks often lead to underutilized hardware, prolonged training times, and restricted model scalability. For machine learning practitioners, understanding and implementing pipeline optimizations enables training of larger models, faster experimentation cycles, and more efficient use of available computing resources.
Here, we explore three widely adopted optimization strategies that address key performance bottlenecks in training pipelines:
- Prefetching and Overlapping: Techniques to minimize data transfer delays and maximize GPU utilization.
- Mixed-Precision Training: A method to reduce memory demands and computational load using lower precision formats.
- Gradient Accumulation and Checkpointing: Strategies to overcome memory limitations during backpropagation and parameter updates.
Each technique is discussed in detail, covering its mechanics, advantages, and practical considerations.
8.5.1 Prefetching and Overlapping
Training machine learning models involves significant data movement between storage, memory, and computational units. The data pipeline consists of sequential transfers: from disk storage to CPU memory, CPU memory to GPU memory, and through the GPU processing units. In standard implementations, each transfer must complete before the next begins, as shown in Figure 8.7, resulting in computational inefficiencies.
\begin{tikzpicture}[font=\small\sf,node distance=0pt]
\tikzset{
Box/.style={inner xsep=2pt,
draw=black!80, line width=0.75pt,
fill=black!10,
anchor=south,
rounded corners=2pt,
font=\sf\fontsize{7pt}{7pt}\selectfont,
%text width=27mm,
align=center,
minimum width=9.5mm,
minimum height=5mm
},
}
\definecolor{col1}{RGB}{240,240,255}
\definecolor{col2}{RGB}{255, 255, 205}
\def\du{205mm}
\def\vi{8mm}
\node[fill=green!10,draw=none,minimum width=\du,
name path=G4,
anchor=south west, minimum height=\vi](B1)at(-19.0mm,3mm){};
\node[right=2mm of B1.west,anchor=west,align=left]{Epoch};
\node[fill=col2,draw=none,minimum width=\du,
name path=G3,
anchor=south west, minimum height=\vi](Z)at(B1.north west){};
\node[right=2mm of Z.west,anchor=west,align=left]{Train};
\node[fill=red!10,draw=none,minimum width=\du,
name path=G2,
anchor=south west, minimum height=\vi](B2)at (Z.north west){};
\node[right=2mm of B2.west,anchor=west,align=left]{Read};
\node[fill=col1,draw=none,minimum width=\du,
name path=G1,
anchor=south west, minimum height=\vi](V)at(B2.north west){};
\node[right= 2mmof V.west,anchor=west,align=left]{Open};
\def\hi{3.95}
\draw[thick,name path=V0](0,0)node[below]{00:00}--++(90:\hi);
\draw[thick,name path=V1](3,0)node[below]{00:15}--++(90:\hi);
\draw[thick,name path=V2](6,0)node[below]{00:30}--++(90:\hi);
\draw[thick,name path=V3](9,0)node[below]{00:45}--++(90:\hi);
\draw[thick,name path=V4](12,0)node[below]{01:00}--++(90:\hi);
\draw[thick,name path=V5](15,0)node[below]{01:15}--++(90:\hi);
\draw[thick,name path=V6](18,0)node[below]{01:30}--++(90:\hi);
%%%%%%%%%%%
\path [name intersections={of=V0 and G1,by={A1,B1}}];
\node[Box, anchor=west]at($(B1)!0.5!(A1)$){Open 1};
\path [name intersections={of=V0 and G2,by={A2,B2}}];
\node[Box, anchor=west,fill=cyan!20]at([xshift=30]$(B2)!0.5!(A2)$){Read 1};
\path [name intersections={of=V0 and G4,by={A3,B3}}];
\node[Box, anchor=west,fill=orange!30, minimum width=80mm, ]at($(B3)!0.5!(A3)$){Epoch 1};
%%
\path [name intersections={of=V1 and G2,by={C1,D1}}];
\node[Box, anchor=west,fill=cyan!20]at([xshift=0]$(C1)!0.5!(D1)$){Read 2};
\path [name intersections={of=V1 and G3,by={C2,D2}}];
\node[Box, anchor=east,fill=magenta!20]at([xshift=0]$(C2)!0.5!(D2)$){Train 1};
\node[Box, anchor=west,fill=magenta!20]at([xshift=30]$(C2)!0.5!(D2)$){Train 2};
%%
\path [name intersections={of=V2 and G2,by={E1,F1}}];
\node[Box, anchor=east,fill=cyan!20]at([xshift=0]$(E1)!0.5!(F1)$){Read 3};
\path [name intersections={of=V2 and G3,by={C3,D3}}];
\node[Box, anchor=west,fill=magenta!20]at([xshift=0]$(C3)!0.5!(D3)$){Train 3};
%
\path [name intersections={of=V4 and G1,by={G1,H1}}];
\node[Box, anchor=east]at([xshift=-30]$(G1)!0.5!(H1)$){Open 2};
\path [name intersections={of=V4 and G2,by={G2,H2}}];
\node[Box, anchor=east,fill=cyan!20]at([xshift=0]$(G2)!0.5!(H2)$){Read 4};
\node[Box, anchor=east,fill=cyan!20]at([xshift=56]$(G2)!0.5!(H2)$){Read 5};
\path [name intersections={of=V4 and G3,by={G3,H3}}];
\node[Box, anchor=west,fill=magenta!20]at([xshift=0]$(G3)!0.5!(H3)$){Train 4};
\path [name intersections={of=V4 and G4,by={G4,H4}}];
\node[Box, anchor=west,fill=orange!30, minimum width=80.5mm]
at([xshift=-59]$(G4)!0.5!(H4)$){Epoch 2};
%
\path [name intersections={of=V5 and G2,by={I1,J1}}];
\node[Box, anchor=west,fill=cyan!20]at([xshift=0]$(I1)!0.5!(J1)$){Read 6};
\path [name intersections={of=V5 and G3,by={I2,J2}}];
\node[Box, anchor=east,fill=magenta!20]at([xshift=0]$(I2)!0.5!(J2)$){Train 5};
\node[Box, anchor=east,fill=magenta!20]at([xshift=59]$(I2)!0.5!(J2)$){Train 6};
\end{tikzpicture}Prefetching addresses these inefficiencies by loading data into memory before its scheduled computation time. During the processing of the current batch, the system loads and prepares subsequent batches, maintaining a consistent supply of ready data (Abadi et al. 2015).
Abadi, Martín, Ashish Agarwal, Paul Barham, et al. 2015. “TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems.” Google Brain.
Overlapping builds upon prefetching by coordinating multiple pipeline stages to execute concurrently. The system processes the current batch while simultaneously preparing future batches through data loading and preprocessing operations. This coordination establishes a continuous data flow through the training pipeline, as illustrated in Figure 8.8.
\begin{tikzpicture}[font=\small\sf,node distance=0pt]
\tikzset{
Box/.style={inner xsep=0pt,
draw=black!80, line width=0.75pt,
fill=black!10,
anchor=south,
rounded corners=2pt,
font=\sf\fontsize{5pt}{5pt}\selectfont,
%text width=27mm,
align=center,
minimum width=20mm,
minimum height=4mm
},
}
\definecolor{col1}{RGB}{240,240,255}
\definecolor{col2}{RGB}{255, 255, 205}
\def\du{205mm}
\def\vi{7mm}
\node[fill=green!10,draw=none,minimum width=\du,
name path=G4,
anchor=south west, minimum height=\vi](B1)at(-19.0mm,3mm){};
\node[right=2mm of B1.west,anchor=west,align=left]{Epoch};
\node[fill=col2,draw=none,minimum width=\du,
name path=G3,
anchor=south west, minimum height=\vi](Z)at(B1.north west){};
\node[right=2mm of Z.west,anchor=west,align=left]{Train};
\node[fill=red!10,draw=none,minimum width=\du,
name path=G2,
anchor=south west, minimum height=\vi](B2)at (Z.north west){};
\node[right=2mm of B2.west,anchor=west,align=left]{Read};
\node[fill=col1,draw=none,minimum width=\du,
name path=G1,
anchor=south west, minimum height=\vi](V)at(B2.north west){};
\node[right= 2mmof V.west,anchor=west,align=left]{Open};
\def\hi{3.45}
\draw[thick,name path=V0](0,0)node[below]{00:00}--++(90:\hi);
\draw[thick,name path=V1](1,0)node[below]{00:05}--++(90:\hi);
\draw[thick,name path=V2](2,0)node[below]{00:10}--++(90:\hi);
%
\draw[thick,name path=V3](3,0)node[below]{00:15}--++(90:\hi);
\draw[thick,name path=V4](4,0)node[below]{00:20}--++(90:\hi);
\draw[thick,name path=V5](5,0)node[below]{00:25}--++(90:\hi);
%
\draw[thick,name path=V6](6,0)node[below]{00:30}--++(90:\hi);
\draw[thick,name path=V7](7,0)node[below]{00:35}--++(90:\hi);
\draw[thick,name path=V8](8,0)node[below]{00:40}--++(90:\hi);
\draw[thick,name path=V9](9,0)node[below]{00:45}--++(90:\hi);
\draw[thick,name path=V10](10,0)node[below]{00:50}--++(90:\hi);
\draw[thick,name path=V11](11,0)node[below]{00:55}--++(90:\hi);
\draw[thick,name path=V12](12,0)node[below]{01:00}--++(90:\hi);
\draw[thick,name path=V13](13,0)node[below]{01:05}--++(90:\hi);
\draw[thick,name path=V14](14,0)node[below]{01:10}--++(90:\hi);
\draw[thick,name path=V15](15,0)node[below]{01:15}--++(90:\hi);
\draw[thick,name path=V16](16,0)node[below]{01:20}--++(90:\hi);
\draw[thick,name path=V17](17,0)node[below]{01:25}--++(90:\hi);
\draw[thick,name path=V18](18,0)node[below]{01:30}--++(90:\hi);
%
\path [name intersections={of=V0 and G1,by={A1,B1}}];
\node[Box, anchor=west,
minimum width=11.2](O1)at($(B1)!0.5!(A1)$){};
\draw[](O1)--++(60:0.5)node[above,inner sep=1pt,
font=\sf\fontsize{6pt}{6pt}\selectfont]{Open 1};
%
\path [name intersections={of=V0 and G2,by={C1,D1}}];
\node[Box, anchor=west, minimum width=16.8,
fill=cyan!20](R1)at([xshift=11.2]$(C1)!0.5!(D1)$){Read 1};
%
\path [name intersections={of=V1 and G2,by={E1,F1}}];
\node[Box, anchor=west, minimum width=11.2,
fill=cyan!20]at([xshift=0]$(E1)!0.5!(F1)$)(R2){};
\draw[](R2)--++(70:0.6)node[above,inner sep=1pt,
font=\sf\fontsize{6pt}{6pt}\selectfont]{Read 2};
\node[Box, anchor=west, minimum width=16.8,
right=-0.5pt of R2,fill=cyan!20]{Read 3};
%
\path [name intersections={of=V1 and G3,by={G1,H1}}];
\node[Box, anchor=west,fill=magenta!20,
minimum width=11.2]at([xshift=0]$(G1)!0.5!(H1)$)(T1){};
\draw[](T1)--++(170:0.45)node[left,inner sep=1pt,
font=\sf\fontsize{6pt}{6pt}\selectfont]{Train 1};
%
\node[Box, anchor=west,fill=magenta!20,
right=-0.5ptof T1,minimum width=16.8](T2){Train 2};
\node[Box, anchor=west,fill=magenta!20,
right=-0.5ptof T2,minimum width=11.2](T3){};
\draw[](T3)--++(40:0.45)node[above,inner sep=1pt,
font=\sf\fontsize{6pt}{6pt}\selectfont]{Train 3};
%
\path [name intersections={of=V0 and G4,by={A3,B3}}];
\node[Box, anchor=west,fill=orange!30,
minimum width=85](E1)at($(B3)!0.5!(A3)$){Epoch 1};
%%%%%%
\path [name intersections={of=V5 and G1,by={I1,J1}}];
\node[Box, anchor=west,
minimum width=11.2](O2)at($(I1)!0.5!(J1)$){};
\draw[](O2)--++(60:0.5)node[above,inner sep=1pt,
font=\sf\fontsize{6pt}{6pt}\selectfont]{Open 2};
%%%
\path [name intersections={of=V5 and G2,by={K1,L1}}];
\node[Box, anchor=west, minimum width=16.8,
fill=cyan!20]at([xshift=11.2]$(K1)!0.5!(L1)$){Read 4};
%
\path [name intersections={of=V6 and G2,by={M1,N1}}];
\node[Box, anchor=west, minimum width=11.2,
fill=cyan!20]at([xshift=0]$(M1)!0.5!(N1)$)(R5){};
\draw[](R5)--++(70:0.6)node[above,inner sep=1pt,
font=\sf\fontsize{6pt}{6pt}\selectfont]{Read 5};
\node[Box, anchor=west, minimum width=16.8,
right=-0.5pt of R5,fill=cyan!20]{Read 6};
%%%%
\path [name intersections={of=V6 and G3,by={O1,P1}}];
\node[Box, anchor=west,fill=magenta!20,
minimum width=11.2]at([xshift=0]$(O1)!0.5!(P1)$)(T4){};
\draw[](T4)--++(170:0.45)node[left,inner sep=1pt,
font=\sf\fontsize{6pt}{6pt}\selectfont]{Train 4};
\node[Box, anchor=west,fill=magenta!20,
right=-0.5pt of T4,minimum width=16.8](T5){Train 5};
\node[Box, anchor=west,fill=magenta!20,
right=-0.5pt of T5,minimum width=11.2](T6){};
\draw[](T6)--++(40:0.45)node[above,inner sep=1pt,
font=\sf\fontsize{6pt}{6pt}\selectfont]{Train 6};
%
\path [name intersections={of=V5 and G4,by={R3,S3}}];
\node[Box, anchor=west,fill=orange!30,
minimum width=85]at($(R3)!0.5!(S3)$){Epoch 2};
\end{tikzpicture}These optimization techniques demonstrate particular value in scenarios involving large-scale datasets, preprocessing-intensive data, multi-GPU training configurations, or high-latency storage systems. The following section examines the specific mechanics of implementing these techniques in modern training systems.
Mechanics
Prefetching and overlapping optimize the training pipeline by enabling different stages of data processing and computation to operate concurrently rather than sequentially. These techniques maximize resource utilization by addressing bottlenecks in data transfer and preprocessing.
As you recall, training data undergoes three main stages: retrieval from storage, transformation into a suitable format, and utilization in model training. An unoptimized pipeline executes these stages sequentially. The GPU remains idle during data fetching and preprocessing, waiting for data preparation to complete. This sequential execution creates significant inefficiencies in the training process.
Prefetching eliminates waiting time by loading data asynchronously during model computation. Data loaders operate as separate threads or processes, preparing the next batch while the current batch trains. This ensures immediate data availability for the GPU when the current batch completes.
Overlapping extends this efficiency by coordinating all three pipeline stages simultaneously. As the GPU processes one batch, preprocessing begins on the next batch, while data fetching starts for the subsequent batch. This coordination maintains constant activity across all pipeline stages.
Modern machine learning frameworks implement these techniques through built-in utilities. PyTorch’s DataLoader class demonstrates this implementation:
loader = DataLoader(dataset,
batch_size=32,
num_workers=4,
prefetch_factor=2)The parameters num_workers and prefetch_factor control parallel processing and data buffering. Multiple worker processes handle data loading and preprocessing concurrently, while prefetch_factor determines the number of batches prepared in advance.
Buffer management plays a key role in pipeline efficiency. The prefetch buffer size requires careful tuning to balance resource utilization. A buffer that is too small causes the GPU to wait for data preparation, reintroducing the idle time these techniques aim to eliminate. Conversely, allocating an overly large buffer consumes memory that could otherwise store model parameters or larger batch sizes.
The implementation relies on effective CPU-GPU coordination. The CPU manages data preparation tasks while the GPU handles computation. This division of labor, combined with storage I/O operations, creates an efficient pipeline that minimizes idle time across hardware resources.
These optimization techniques yield particular benefits in scenarios involving slow storage access, complex data preprocessing, or large datasets. The next section examines the specific advantages these techniques offer in different training contexts.
Benefits
Prefetching and overlapping are powerful techniques that significantly enhance the efficiency of training pipelines by addressing key bottlenecks in data handling and computation. To illustrate the impact of these benefits, Table 8.4 presents the following comparison:
| Aspect | Traditional Pipeline | With Prefetching & Overlapping |
|---|---|---|
| GPU Utilization | Frequent idle periods | Near-constant utilization |
| Training Time | Longer due to sequential operations | Reduced through parallelism |
| Resource Usage | Often suboptimal | Maximized across available hardware |
| Scalability | Limited by slowest component | Adaptable to various bottlenecks |
One of the most critical advantages of these methods is the improvement in GPU utilization. In traditional, unoptimized pipelines, the GPU often remains idle while waiting for data to be fetched and preprocessed. This idle time creates inefficiencies, especially in workflows where data augmentation or preprocessing involves complex transformations. By introducing asynchronous data loading and overlapping, these techniques ensure that the GPU consistently has data ready to process, eliminating unnecessary delays.
Another important benefit is the reduction in overall training time. Prefetching and overlapping allow the computational pipeline to operate continuously, with multiple stages working simultaneously rather than sequentially. For example, while the GPU processes the current batch, the data loader fetches and preprocesses the next batch, ensuring a steady flow of data through the system. This parallelism minimizes latency between training iterations, allowing for faster completion of training cycles, particularly in scenarios involving large-scale datasets.
Additionally, these techniques are highly scalable and adaptable to various hardware configurations. Prefetching buffers and overlapping mechanisms can be tuned to match the specific requirements of a system, whether the bottleneck lies in slow storage, limited network bandwidth, or computational constraints. By aligning the data pipeline with the capabilities of the underlying hardware, prefetching and overlapping maximize resource utilization, making them invaluable for large-scale machine learning workflows.
Overall, prefetching and overlapping directly address some of the most common inefficiencies in training pipelines. By optimizing data flow and computation, these methods not only improve hardware efficiency but also enable the training of more complex models within shorter timeframes.
Use Cases
Prefetching and overlapping are highly versatile techniques that can be applied across various machine learning domains and tasks to enhance pipeline efficiency. Their benefits are most evident in scenarios where data handling and preprocessing are computationally expensive or where large-scale datasets create potential bottlenecks in data transfer and loading.
One of the primary use cases is in computer vision, where datasets often consist of high-resolution images requiring extensive preprocessing. Tasks such as image classification, object detection, or semantic segmentation typically involve operations like resizing, normalization, and data augmentation, all of which can significantly increase preprocessing time. By employing prefetching and overlapping, these operations can be carried out concurrently with computation, ensuring that the GPU remains busy during the training process.
For example, a typical image classification pipeline might include random cropping (10 ms), color jittering (15 ms), and normalization (5 ms). Without prefetching, these 30ms of preprocessing would delay each training step. Prefetching allows these operations to occur during the previous batch’s computation.
Natural language processing (NLP) workflows also benefit from these techniques, particularly when working with large corpora of text data. For instance, preprocessing text data involves tokenization (converting words to numbers), padding sequences to equal length, and potentially subword tokenization. In a BERT model training pipeline, these steps might process thousands of sentences per batch. Prefetching allows this text processing to happen concurrently with model training. Prefetching ensures that these transformations occur in parallel with training, while overlapping optimizes data transfer and computation. This is especially useful in transformer-based models like BERT or GPT, which require consistent throughput to maintain efficiency given their high computational demand.
Distributed training systems, which we will discuss next, involve multiple GPUs or nodes, present another critical application for prefetching and overlapping. In distributed setups, network latency and data transfer rates often become the primary bottleneck. Prefetching mitigates these issues by ensuring that data is ready and available before it is required by any specific GPU. Overlapping further optimizes distributed training pipelines by coordinating the data preprocessing on individual nodes while the central computation continues, thus reducing overall synchronization delays.
Beyond these domains, prefetching and overlapping are particularly valuable in workflows involving large-scale datasets stored on remote or cloud-based systems. When training on cloud platforms, the data may need to be fetched over a network or from distributed storage, which introduces additional latency. Using prefetching and overlapping in such cases helps minimize the impact of these delays, ensuring that training proceeds smoothly despite slower data access speeds.
These use cases illustrate how prefetching and overlapping address inefficiencies in various machine learning pipelines. By optimizing the flow of data and computation, these techniques enable faster, more reliable training workflows across a wide range of applications.
Challenges and Trade-offs
While prefetching and overlapping are powerful techniques for optimizing training pipelines, their implementation comes with certain challenges and trade-offs. Understanding these limitations is crucial for effectively applying these methods in real-world machine learning workflows.
One of the primary challenges is the increased memory usage that accompanies prefetching and overlapping. By design, these techniques rely on maintaining a buffer of prefetched data batches, which requires additional memory resources. For large datasets or high-resolution inputs, this memory demand can become significant, especially when training on GPUs with limited memory capacity. If the buffer size is not carefully tuned, it may lead to out-of-memory errors, forcing practitioners to reduce batch sizes or adjust other parameters, which can impact overall efficiency.
For example, with a prefetch factor of 2 and batch size of 256 high-resolution images (\(1024\times1024\) pixels), the buffer might require an additional 2GB of GPU memory. This becomes particularly challenging when training vision models that already require significant memory for their parameters and activations.
Another difficulty lies in tuning the parameters that control prefetching and overlapping. Settings such as num_workers and prefetch_factor in PyTorch, or buffer sizes in other frameworks, need to be optimized for the specific hardware and workload. For instance, increasing the number of worker threads can improve throughput up to a point, but beyond that, it may lead to contention for CPU resources or even degrade performance due to excessive context switching. Determining the optimal configuration often requires empirical testing, which can be time-consuming. A common starting point is to set num_workers to the number of CPU cores available. However, on a 16-core system processing large images, using all cores for data loading might leave insufficient CPU resources for other essential operations, potentially slowing down the entire pipeline.
Debugging also becomes more complex in pipelines that employ prefetching and overlapping. Asynchronous data loading and multithreading or multiprocessing introduce potential race conditions, deadlocks, or synchronization issues. Diagnosing errors in such systems can be challenging because the execution flow is no longer straightforward. Developers may need to invest additional effort into monitoring, logging, and debugging tools to ensure that the pipeline operates reliably.
Moreover, there are scenarios where prefetching and overlapping may offer minimal benefits. For instance, in systems where storage access or network bandwidth is significantly faster than the computation itself, these techniques might not noticeably improve throughput. In such cases, the additional complexity and memory overhead introduced by prefetching may not justify its use.
Finally, prefetching and overlapping require careful coordination across different components of the training pipeline, such as storage, CPUs, and GPUs. Poorly designed pipelines can lead to imbalances where one stage becomes a bottleneck, negating the advantages of these techniques. For example, if the data loading process is too slow to keep up with the GPU’s processing speed, the benefits of overlapping will be limited.
Despite these challenges, prefetching and overlapping remain essential tools for optimizing training pipelines when used appropriately. By understanding and addressing their trade-offs, practitioners can implement these techniques effectively, ensuring smoother and more efficient machine learning workflows.
8.5.2 Mixed-Precision Training
Mixed-precision training combines different numerical precisions during model training to optimize computational efficiency. This approach uses combinations of 32-bit floating-point (FP32), 16-bit floating-point (FP16), and brain floating-point (bfloat16) formats to reduce memory usage and speed up computation while preserving model accuracy (Micikevicius et al. 2017a; Wang and Kanwar 2019).
Micikevicius, Paulius, Sharan Narang, Jonah Alben, Gregory Diamos, Erich Elsen, David Garcia, Boris Ginsburg, et al. 2017a. “Mixed Precision Training.” arXiv Preprint arXiv:1710.03740, October. http://arxiv.org/abs/1710.03740v3.
Wang, Y., and P. Kanwar. 2019. “BFloat16: The Secret to High Performance on Cloud TPUs.” Google Cloud Blog.
A neural network trained in FP32 requires 4 bytes per parameter, while both FP16 and bfloat16 use 2 bytes. For a model with \(10^9\) parameters, this reduction cuts memory usage from 4 GB to 2 GB. This memory reduction enables larger batch sizes and deeper architectures on the same hardware.
The numerical precision differences between these formats shape their use cases. FP32 represents numbers from approximately \(\pm1.18 \times 10^{-38}\) to \(\pm3.4 \times 10^{38}\) with 7 decimal digits of precision. FP16 ranges from \(\pm6.10 \times 10^{-5}\) to \(\pm65,504\) with 3-4 decimal digits of precision. Bfloat16, developed by Google Brain, maintains the same dynamic range as FP32 (\(\pm1.18 \times 10^{-38}\) to \(\pm3.4 \times 10^{38}\)) but with reduced precision (3-4 decimal digits). This range preservation makes bfloat16 particularly suited for deep learning training, as it handles large and small gradients more effectively than FP16.
The hybrid approach proceeds in three main phases, as illustrated in Figure 8.9. During the forward pass, input data converts to reduced precision (FP16 or bfloat16), and matrix multiplications execute in this format, including activation function computations. In the gradient computation phase, the backward pass calculates gradients in reduced precision, but results are stored in FP32 master weights. Finally, during weight updates, the optimizer updates the main weights in FP32, and these updated weights convert back to reduced precision for the next forward pass.
\scalebox{0.8}{
\begin{tikzpicture}[font=\small\sf,node distance=7mm]
\definecolor{col1}{RGB}{128, 179, 255}
\definecolor{col2}{RGB}{255, 255, 128}
\definecolor{col3}{RGB}{204, 255, 204}
\definecolor{col5}{RGB}{170,170,51}
\definecolor{col6}{RGB}{245, 82, 102}
\definecolor{col7}{RGB}{72,84,69}
\definecolor{col4}{RGB}{229,255,229}
\tikzset{
Box/.style={inner xsep=2pt,
draw=col7, line width=0.75pt,
fill=col4!90,
anchor=west,
text width=27mm,align=center,
minimum width=27mm, minimum height=10mm
},
}
\node[Box](B1){Model FP16};
\node[Box,below=of B1](B2){Gradients FP16};
\node[Box,below=of B2](B3){Gradients FP32};
\node[Box,below=of B3](B4){Optimizer Core FP32};
\node[Box,below=of B3](B4){Weights FP32};
\node[Box,below=of B4](B5){Weights FP16};
\scoped[on background layer]
\node[draw=col5,inner xsep=10mm,
line width=0.75pt,
inner ysep=4mm,
fill=col2!10,yshift=1mm,
fit=(B2)(B4)](BB){};
\node[below=1pt of BB.north west,anchor=north west]{Optimizer};
%
\draw[-latex](B1)--(B2);
\draw[-latex](B2)--(B3);
\draw[-latex](B3)--(B4);
\draw[-latex](B4)--(B5);
\draw[-latex](B1.east)--++(0:14mm)|-(B5);
\end{tikzpicture}}Modern hardware architectures are specifically designed to accelerate reduced precision computations. GPUs from NVIDIA include Tensor Cores4 optimized for FP16 and bfloat16 operations (Jia et al. 2018). Google’s TPUs natively support bfloat16, as this format was specifically designed for machine learning workloads. These architectural optimizations typically enable an order of magnitude higher computational throughput for reduced precision operations compared to FP32, making mixed-precision training particularly efficient on modern hardware.
4 Tensor Cores: NVIDIA GPU units that accelerate matrix operations with reduced precision formats like FP16 and bfloat16, boosting deep learning performance by enabling parallel computations.
Jia, Xianyan, Shutao Song, Wei He, Yangzihao Wang, Haidong Rong, Feihu Zhou, Liqiang Xie, et al. 2018. “Highly Scalable Deep Learning Training System with Mixed-Precision: Training ImageNet in Four Minutes.” arXiv Preprint arXiv:1807.11205, July. http://arxiv.org/abs/1807.11205v1.
FP16 Computation
The majority of operations in mixed-precision training, such as matrix multiplications and activation functions, are performed in FP16. The reduced precision allows these calculations to be executed faster and with less memory consumption compared to FP32. FP16 operations are particularly effective on modern GPUs equipped with Tensor Cores, which are designed to accelerate computations involving half-precision values. These cores perform FP16 operations natively, resulting in significant speedups.
FP32 Accumulation
While FP16 is efficient, its limited precision can lead to numerical instability, especially in critical operations like gradient updates. To mitigate this, mixed-precision training retains FP32 precision for certain steps, such as weight updates and gradient accumulation. By maintaining higher precision for these calculations, the system avoids the risk of gradient underflow or overflow, ensuring the model converges correctly during training.
Loss Scaling
One of the key challenges with FP16 is its reduced dynamic range, which increases the likelihood of gradient values becoming too small to be represented accurately. Loss scaling addresses this issue by temporarily amplifying gradient values during backpropagation. Specifically, the loss value is scaled by a large factor (e.g., \(2^{10}\)) before gradients are computed, ensuring they remain within the representable range of FP16. Once the gradients are computed, the scaling factor is reversed during the weight update step to restore the original gradient magnitude. This process allows FP16 to be used effectively without sacrificing numerical stability.
Modern machine learning frameworks, such as PyTorch and TensorFlow, provide built-in support for mixed-precision training. These frameworks abstract the complexities of managing different precisions, enabling practitioners to implement mixed-precision workflows with minimal effort. For instance, PyTorch’s torch.cuda.amp (Automatic Mixed Precision) library automates the process of selecting which operations to perform in FP16 or FP32, as well as applying loss scaling when necessary.
Combining FP16 computation, FP32 accumulation, and loss scaling allows us to achieve mixed-precision training, resulting in a significant reduction in memory usage and computational overhead without compromising the accuracy or stability of the training process. The following sections will explore the practical advantages of this approach and its impact on modern machine learning workflows.
Benefits
Mixed-precision training offers several significant advantages that make it an essential optimization technique for modern machine learning workflows. By reducing memory usage and computational load, it enables practitioners to train larger models, process bigger batches, and achieve faster results, all while maintaining model accuracy and convergence.
One of the most prominent benefits of mixed-precision training is its substantial reduction in memory consumption. FP16 computations require only half the memory of FP32 computations, which directly reduces the storage required for activations, weights, and gradients during training. For instance, a transformer model with 1 billion parameters requires 4 GB of memory for weights in FP32, but only 2GB in FP16. This memory efficiency allows for larger batch sizes, which can lead to more stable gradient estimates and faster convergence. Additionally, with less memory consumed per operation, practitioners can train deeper and more complex models on the same hardware, unlocking capabilities that were previously limited by memory constraints.
Another key advantage is the acceleration of computations. Modern GPUs, such as those equipped with Tensor Cores, are specifically optimized for FP16 operations. These cores enable hardware to process more operations per cycle compared to FP32, resulting in faster training times. For matrix multiplication operations, which constitute 80-90% of training computation time in large models, FP16 can achieve 2-3\(\times\) speedup compared to FP32. This computational speedup becomes particularly noticeable in large-scale models, such as transformers and convolutional neural networks, where matrix multiplications dominate the workload.
Mixed-precision training also improves hardware utilization by better matching the capabilities of modern accelerators. In traditional FP32 workflows, the computational throughput of GPUs is often underutilized due to their design for parallel processing. FP16 operations, being less demanding, allow more computations to be performed simultaneously, ensuring that the hardware operates closer to its full capacity.
Finally, mixed-precision training aligns well with the requirements of distributed and cloud-based systems. In distributed training, where large-scale models are trained across multiple GPUs or nodes, memory and bandwidth become critical constraints. By reducing the size of tensors exchanged between devices, mixed precision not only speeds up inter-device communication but also decreases overall resource demands. This makes it particularly effective in environments where scalability and cost-efficiency are priorities.
Overall, the benefits of mixed-precision training extend beyond performance improvements. By optimizing memory usage and computation, this technique empowers machine learning practitioners to train cutting-edge models more efficiently, making it a cornerstone of modern machine learning.
Use Cases
Mixed-precision training has become a essential in machine learning workflows, particularly in domains and scenarios where computational efficiency and memory optimization are critical. Its ability to enable faster training and larger model capacities makes it highly applicable across a variety of machine learning tasks and architectures.
One of the most prominent use cases is in training large-scale machine learning models. In natural language processing (NLP), models such as BERT (345M parameters), GPT-3 (175B parameters), and Transformer-based architectures involve extensive matrix multiplications and large parameter sets. Mixed-precision training allows these models to operate with larger batch sizes or deeper configurations, facilitating faster convergence and improved accuracy on massive datasets.
In computer vision, tasks such as image classification, object detection, and segmentation often require handling high-resolution images and applying computationally intensive convolutional operations. By leveraging mixed-precision training, these workloads can be executed more efficiently, enabling the training of advanced architectures like ResNet, EfficientNet, and vision transformers within practical resource limits.
Mixed-precision training is also particularly valuable in reinforcement learning (RL), where models interact with environments to optimize decision-making policies. RL often involves high-dimensional state spaces and requires substantial computational resources for both model training and simulation. Mixed precision reduces the overhead of these processes, allowing researchers to focus on larger environments and more complex policy networks.
Another critical application is in distributed training systems. When training models across multiple GPUs or nodes, memory and bandwidth become limiting factors for scalability. Mixed precision addresses these issues by reducing the size of activations, weights, and gradients exchanged between devices. For example, in a distributed training setup with 8 GPUs, reducing tensor sizes from FP32 to FP16 can halve the communication bandwidth requirements from 320 GB/s to 160 GB/s. This optimization is especially beneficial in cloud-based environments, where resource allocation and cost efficiency are paramount.
Additionally, mixed-precision training is increasingly used in areas such as speech processing, generative modeling, and scientific simulations. Models in these fields often have large data and parameter requirements that can push the limits of traditional FP32 workflows. By optimizing memory usage and leveraging the speedups provided by Tensor Cores, practitioners can train state-of-the-art models faster and more cost-effectively.
The adaptability of mixed-precision training to diverse tasks and domains underscores its importance in modern machine learning. Whether applied to large-scale natural language models, computationally intensive vision architectures, or distributed training environments, this technique empowers researchers and engineers to push the boundaries of what is computationally feasible.
Challenges and Trade-offs
While mixed-precision training offers significant advantages in terms of memory efficiency and computational speed, it also introduces several challenges and trade-offs that must be carefully managed to ensure successful implementation.
One of the primary challenges lies in the reduced precision of FP16. While FP16 computations are faster and require less memory, their limited dynamic range \((\pm65,504)\) can lead to numerical instability, particularly during gradient computations. Small gradient values below \(6 \times 10^{-5}\) become too small to be represented accurately in FP16, resulting in underflow. While loss scaling addresses this by multiplying gradients by factors like \(2^{8}\) to \(2^{14}\), implementing and tuning this scaling factor adds complexity to the training process.
Another trade-off involves the increased risk of convergence issues. While many modern machine learning tasks perform well with mixed-precision training, certain models or datasets may require higher precision to achieve stable and reliable results. For example, recurrent neural networks with long sequences often accumulate numerical errors in FP16, requiring careful gradient clipping and precision management. In such cases, practitioners may need to experiment with selectively enabling or disabling FP16 computations for specific operations, which can complicate the training workflow.
Debugging and monitoring mixed-precision training also require additional attention. Numerical issues such as NaN (Not a Number) values in gradients or activations are more common in FP16 workflows and may be difficult to trace without proper tools and logging. For instance, gradient explosions in deep networks might manifest differently in mixed precision, appearing as infinities in FP16 before they would in FP32. Frameworks like PyTorch and TensorFlow provide utilities for debugging mixed-precision training, but these tools may not catch every edge case, especially in custom implementations.
Another challenge is the dependency on specialized hardware. Mixed-precision training relies heavily on GPU architectures optimized for FP16 operations, such as Tensor Cores in NVIDIA’s GPUs. While these GPUs are becoming increasingly common, not all hardware supports mixed-precision operations, limiting the applicability of this technique in some environments.
Finally, there are scenarios where mixed-precision training may not provide significant benefits. Models with relatively low computational demand (less than 10M parameters) or small parameter sizes may not fully utilize the speedups offered by FP16 operations. In such cases, the additional complexity of mixed-precision workflows may outweigh their potential advantages.
Despite these challenges, mixed-precision training remains a highly effective optimization technique for most large-scale machine learning tasks. By understanding and addressing its trade-offs, practitioners can harness its benefits while minimizing potential drawbacks, ensuring efficient and reliable training workflows.
8.5.3 Gradient Accumulation and Checkpointing
Training large machine learning models often requires significant memory resources, particularly for storing three key components: activations (intermediate layer outputs), gradients (parameter updates), and model parameters (weights and biases) during forward and backward passes. However, memory constraints on GPUs can limit the batch size or the complexity of models that can be trained on a given device.
Gradient accumulation and activation checkpointing are two techniques designed to address these limitations by optimizing how memory is utilized during training. Both techniques enable researchers and practitioners to train larger and more complex models, making them indispensable tools for modern deep learning workflows. In the following sections, we will go deeper into the mechanics of gradient accumulation and activation checkpointing, exploring their benefits, use cases, and practical implementation.
Mechanics
Gradient accumulation and activation checkpointing operate on distinct principles, but both aim to optimize memory usage during training by modifying how forward and backward computations are handled.
Gradient Accumulation
Gradient accumulation simulates larger batch sizes by splitting a single effective batch into smaller “micro-batches.” As illustrated in Figure 8.10, during each forward and backward pass, the gradients for a micro-batch are computed and added to an accumulated gradient buffer. Instead of immediately applying the gradients to update the model parameters, this process repeats for several micro-batches. Once the gradients from all micro-batches in the effective batch are accumulated, the parameters are updated using the combined gradients.
This process allows models to achieve the benefits of training with larger batch sizes, such as improved gradient estimates and convergence stability, without requiring the memory to store an entire batch at once. For instance, in PyTorch, this can be implemented by adjusting the learning rate proportionally to the number of accumulated micro-batches and calling optimizer.step() only after processing the entire effective batch.
The key steps in gradient accumulation are:
- Perform the forward pass for a micro-batch.
- Compute the gradients during the backward pass.
- Accumulate the gradients into a buffer without updating the model parameters.
- Repeat steps 1-3 for all micro-batches in the effective batch.
- Update the model parameters using the accumulated gradients after all micro-batches are processed.
Activation Checkpointing
Activation checkpointing reduces memory usage during the backward pass by discarding and selectively recomputing activations. In standard training, activations from the forward pass are stored in memory for use in gradient computations during backpropagation. However, these activations can consume significant memory, particularly in deep networks.
With checkpointing, only a subset of the activations is retained during the forward pass. When gradients need to be computed during the backward pass, the discarded activations are recomputed on demand by re-executing parts of the forward pass. This approach trades computational efficiency for memory savings, as the recomputation increases training time but allows deeper models to be trained within limited memory constraints.
The implementation involves:
- Splitting the model into segments.
- Retaining activations only at the boundaries of these segments during the forward pass.
- Recomputing activations for intermediate layers during the backward pass when needed.
Frameworks like PyTorch provide tools such as torch.utils.checkpoint to simplify this process. Checkpointing is particularly effective for very deep architectures, such as transformers or large convolutional networks, where the memory required for storing activations can exceed the GPU’s capacity.
The synergy between gradient accumulation and checkpointing enables training of larger, more complex models. Gradient accumulation manages memory constraints related to batch size, while checkpointing optimizes memory usage for intermediate activations. Together, these techniques expand the range of models that can be trained on available hardware.
Benefits
Gradient accumulation and activation checkpointing provide solutions to the memory limitations often encountered in training large-scale machine learning models. By optimizing how memory is used during training, these techniques enable the development and deployment of complex architectures, even on hardware with constrained resources.
One of the primary benefits of gradient accumulation is its ability to simulate larger batch sizes without increasing the memory requirements for storing the full batch. Larger batch sizes are known to improve gradient estimates, leading to more stable convergence and faster training. With gradient accumulation, practitioners can achieve these benefits while working with smaller micro-batches that fit within the GPU’s memory. This flexibility is useful when training models on high-resolution data, such as large images or 3D volumetric data, where even a single batch may exceed available memory.
Activation checkpointing, on the other hand, significantly reduces the memory footprint of intermediate activations during the forward pass. This allows for the training of deeper models, which would otherwise be infeasible due to memory constraints. By discarding and recomputing activations as needed, checkpointing frees up memory that can be used for larger models, additional layers, or higher resolution data. This is especially important in state-of-the-art architectures, such as transformers or dense convolutional networks, which require substantial memory to store intermediate computations.
Both techniques enhance the scalability of machine learning workflows. In resource-constrained environments, such as cloud-based platforms or edge devices, these methods provide a means to train models efficiently without requiring expensive hardware upgrades. Furthermore, they enable researchers to experiment with larger and more complex architectures, pushing the boundaries of what is computationally feasible.
Beyond memory optimization, these techniques also contribute to cost efficiency. By reducing the hardware requirements for training, gradient accumulation and checkpointing lower the overall cost of development, making them valuable for organizations working within tight budgets. This is particularly relevant for startups, academic institutions, or projects running on shared computing resources.
Gradient accumulation and activation checkpointing provide both technical and practical advantages. These techniques create a more flexible, scalable, and cost-effective approach to training large-scale models, empowering practitioners to tackle increasingly complex machine learning challenges.
Use Cases
Gradient accumulation and activation checkpointing are particularly valuable in scenarios where hardware memory limitations present significant challenges during training. These techniques are widely used in training large-scale models, working with high-resolution data, and optimizing workflows in resource-constrained environments.
A common use case for gradient accumulation is in training models that require large batch sizes to achieve stable convergence. For example, models like GPT, BERT, and other transformer architectures often benefit from larger batch sizes due to their improved gradient estimates. However, these batch sizes can quickly exceed the memory capacity of GPUs, especially when working with high-dimensional inputs or multiple GPUs. By accumulating gradients over multiple smaller micro-batches, gradient accumulation enables the use of effective large batch sizes without exceeding memory limits. This is particularly beneficial for tasks like language modeling, sequence-to-sequence learning, and image classification, where batch size significantly impacts training dynamics.
Activation checkpointing enables training of deep neural networks with numerous layers or complex computations. In computer vision, architectures like ResNet-152, EfficientNet, and DenseNet require substantial memory to store intermediate activations during training. Checkpointing reduces this memory requirement through strategic recomputation of activations, making it possible to train these deeper architectures within GPU memory constraints.
In the domain of natural language processing, models like GPT-3 or T5, with hundreds of layers and billions of parameters, rely heavily on checkpointing to manage memory usage. These models often exceed the memory capacity of a single GPU, making checkpointing a necessity for efficient training. Similarly, in generative adversarial networks (GANs), which involve both generator and discriminator models, checkpointing helps manage the combined memory requirements of both networks during training.
Another critical application is in resource-constrained environments, such as edge devices or cloud-based platforms. In these scenarios, memory is often a limiting factor, and upgrading hardware may not always be a viable option. Gradient accumulation and checkpointing provide a cost-effective solution for training models on existing hardware, enabling efficient workflows without requiring additional investment in resources.
These techniques are also indispensable in research and experimentation. They allow practitioners to prototype and test larger and more complex models, exploring novel architectures that would otherwise be infeasible due to memory constraints. This is particularly valuable for academic researchers and startups operating within limited budgets.
Gradient accumulation and activation checkpointing solve fundamental challenges in training large-scale models within memory-constrained environments. These techniques have become essential tools for practitioners in natural language processing, computer vision, generative modeling, and edge computing, enabling broader adoption of advanced machine learning architectures.
Challenges and Trade-offs
While gradient accumulation and activation checkpointing are powerful tools for optimizing memory usage during training, their implementation introduces several challenges and trade-offs that must be carefully managed to ensure efficient and reliable workflows.
One of the primary trade-offs of activation checkpointing is the additional computational overhead it introduces. By design, checkpointing saves memory by discarding and recomputing intermediate activations during the backward pass. This recomputation increases the training time, as portions of the forward pass must be executed multiple times. For example, in a transformer model with 12 layers, if checkpoints are placed every 4 layers, each intermediate activation would need to be recomputed up to three times during the backward pass. The extent of this overhead depends on how the model is segmented for checkpointing and the computational cost of each segment. Practitioners must strike a balance between memory savings and the additional time spent on recomputation, which may affect overall training efficiency.
Gradient accumulation, while effective at simulating larger batch sizes, can lead to slower parameter updates. Since gradients are accumulated over multiple micro-batches, the model parameters are updated less frequently compared to training with full batches. This delay in updates can impact the speed of convergence, particularly in models sensitive to batch size dynamics. Additionally, gradient accumulation requires careful tuning of the learning rate. For instance, if accumulating gradients over 4 micro-batches to simulate a batch size of 128, the learning rate typically needs to be scaled up by a factor of 4 to maintain the same effective learning rate as training with full batches. The effective batch size increases with accumulation, necessitating proportional adjustments to the learning rate to maintain stable training.
Debugging and monitoring are also more complex when using these techniques. In activation checkpointing, errors may arise during recomputation, making it more difficult to trace issues back to their source. Similarly, gradient accumulation requires ensuring that gradients are correctly accumulated and reset after each effective batch, which can introduce bugs if not handled properly.
Another challenge is the increased complexity in implementation. While modern frameworks like PyTorch provide utilities to simplify gradient accumulation and checkpointing, effective use still requires understanding the underlying principles. For instance, activation checkpointing demands segmenting the model appropriately to minimize recomputation overhead while achieving meaningful memory savings. Improper segmentation can lead to suboptimal performance or excessive computational cost.
These techniques may also have limited benefits in certain scenarios. For example, if the computational cost of recomputation in activation checkpointing is too high relative to the memory savings, it may negate the advantages of the technique. Similarly, for models or datasets that do not require large batch sizes, the complexity introduced by gradient accumulation may not justify its use.
Despite these challenges, gradient accumulation and activation checkpointing remain indispensable for training large-scale models under memory constraints. By carefully managing their trade-offs and tailoring their application to specific workloads, practitioners can maximize the efficiency and effectiveness of these techniques.
8.5.4 Comparison
As summarized in Table 8.5, these techniques vary in their implementation complexity, hardware requirements, and impact on computation speed and memory usage. The selection of an appropriate optimization strategy depends on factors such as the specific use case, available hardware resources, and the nature of performance bottlenecks in the training process.
| Aspect | Prefetching and Overlapping | Mixed-Precision Training | Gradient Accumulation and Checkpointing |
|---|---|---|---|
| Primary Goal | Minimize data transfer delays and maximize GPU utilization | Reduce memory consumption and computational overhead | Overcome memory limitations during backpropagation and parameter updates |
| Key Mechanism | Asynchronous data loading and parallel processing | Combining FP16 and FP32 computations | Simulating larger batch sizes and selective activation storage |
| Memory Impact | Increases memory usage for prefetch buffer | Reduces memory usage by using FP16 | Reduces memory usage for activations and gradients |
| Computation Speed | Improves by reducing idle time | Accelerates computations using FP16 | May slow down due to recomputations in checkpointing |
| Scalability | Highly scalable, especially for large datasets | Enables training of larger models | Allows training deeper models on limited hardware |
| Hardware Requirements | Benefits from fast storage and multi-core CPUs | Requires GPUs with FP16 support (e.g., Tensor Cores) | Works on standard hardware |
| Implementation Complexity | Moderate (requires tuning of prefetch parameters) | Low to moderate (with framework support) | Moderate (requires careful segmentation and accumulation) |
| Main Benefits | Reduces training time, improves hardware utilization | Faster training, larger models, reduced memory usage | Enables larger batch sizes and deeper models |
| Primary Challenges | Tuning buffer sizes, increased memory usage | Potential numerical instability, loss scaling needed | Increased computational overhead, slower parameter updates |
| Ideal Use Cases | Large datasets, complex preprocessing | Large-scale models, especially in NLP and computer vision | Very deep networks, memory-constrained environments |
While these three techniques represent core optimization strategies in machine learning, they are part of a larger optimization landscape. Other notable techniques include pipeline parallelism for multi-GPU training, dynamic batching for variable-length inputs, and quantization for inference optimization. Practitioners should evaluate their specific requirements—such as model architecture, dataset characteristics, and hardware constraints—to select the most appropriate combination of optimization techniques for their use case.
8.6 Distributed Training Systems
Thus far, we have focused on ML training pipelines from a single-system perspective. However, training machine learning models often requires scaling beyond a single machine due to increasing model complexity and dataset sizes. The demand for computational power, memory, and storage can exceed the capacity of individual devices, especially in domains like natural language processing, computer vision, and scientific computing. Distributed training addresses this challenge by spreading the workload across multiple machines, which coordinate to train a single model efficiently.
This coordination introduces several fundamental challenges that distributed training systems must address. A distributed training system must orchestrate multi-machine computation by splitting up the work, managing communication between machines, and maintaining synchronization throughout the training process. Understanding these basic requirements provides the foundation for examining the main approaches to distributed training: data parallelism, which divides the training data across machines; model parallelism, which splits the model itself; and hybrid approaches that combine both strategies.
8.6.1 Data Parallelism
Data parallelism is a method for distributing the training process across multiple devices by splitting the dataset into smaller subsets. Each device trains a complete copy of the model using its assigned subset of the data. For example, when training an image classification model on 1 million images using 4 GPUs, each GPU would process 250,000 images while maintaining an identical copy of the model architecture.
Data parallelism is particularly effective when the dataset size is large but the model size is manageable, as each device must store a full copy of the model in memory. This method is widely used in scenarios such as image classification and natural language processing, where the dataset can be processed in parallel without dependencies between data samples. For instance, when training a ResNet model on ImageNet, each GPU can independently process its portion of images since the classification of one image doesn’t depend on the results of another.
Mathematical Foundations
Data parallelism builds on a key insight from stochastic gradient descent. Gradients computed on different minibatches can be averaged. This property enables parallel computation across devices. Let’s examine why this works mathematically.
Consider a model with parameters \(θ\) training on a dataset \(D\). The loss function for a single data point \(x_i\) is \(L(θ, x_i)\). In standard SGD with batch size \(B\), the gradient update for a minibatch is: \[ g = \frac{1}{B} \sum_{i=1}^B \nabla_θ L(θ, x_i) \]
In data parallelism with \(N\) devices, each device \(k\) computes gradients on its own minibatch \(B_k\): \[ g_k = \frac{1}{|B_k|} \sum_{x_i \in B_k} \nabla_θ L(θ, x_i) \]
The global update averages these local gradients: \[ g_{\text{global}} = \frac{1}{N} \sum_{k=1}^N g_k \]
This averaging is mathematically equivalent to computing the gradient on the combined batch \(B_{\text{total}} = \bigcup_{k=1}^N B_k\): \[ g_{\text{global}} = \frac{1}{|B_{\text{total}}|} \sum_{x_i \in B_{\text{total}}} \nabla_θ L(θ, x_i) \]
This equivalence shows why data parallelism maintains the statistical properties of SGD training. The approach distributes distinct data subsets across devices, computes local gradients independently, and averages these gradients to approximate the full-batch gradient.
The method parallels gradient accumulation, where a single device accumulates gradients over multiple forward passes before updating parameters. Both techniques leverage the additive properties of gradients to process large batches efficiently.
Mechanics
The process of data parallelism can be broken into a series of distinct steps, each with its role in ensuring the system operates efficiently. These steps are illustrated in Figure 8.11.
\begin{tikzpicture}[font=\small\sf,node distance=19mm]
\definecolor{col1}{RGB}{128, 179, 255}
\definecolor{col2}{RGB}{255, 255, 128}
\definecolor{col3}{RGB}{204, 255, 204}
\definecolor{col5}{RGB}{170,170,51}
\definecolor{col6}{RGB}{245, 82, 102}
\definecolor{col7}{RGB}{72,84,69}
\definecolor{col4}{RGB}{229,255,229}
\tikzset{
Box/.style={inner xsep=2pt,
draw=col7, line width=0.75pt,
fill=col4!80,
anchor=west,
text width=27mm,align=flush center,
minimum width=27mm, minimum height=10mm
},
}
\tikzset{
Box2/.style={inner xsep=2pt,
draw=col7, line width=0.75pt,
fill=col4!80,
anchor=west,
text width=21mm,align=flush center,
minimum width=22mm, minimum height=10mm
},
}
\tikzset{
Text/.style={inner xsep=2pt,
draw=none, line width=0.75pt,
fill=black!10,
font=\footnotesize\sf,
align=flush center,
minimum width=22mm, minimum height=9mm
},
}
\node[Box,node distance=11mm](B1){GPU 1\\Forward \& Backward Pass};
\node[Box,node distance=11mm,right=of B1](B2){GPU 2\\Forward \& Backward Pass};
\node[Box,node distance=11mm,right=of B2](B3){GPU 3\\Forward \& Backward Pass};
\node[Box,node distance=11mm,right=of B3](B4){GPU 4\\Forward \& Backward Pass};
%
\node[Box2,above=of B1](GB1){Batch 1};
\node[Box2,above=of B2](GB2){Batch 2};
\node[Box2,above=of B3](GB3){Batch 3};
\node[Box2,above=of B4](GB4){Batch 4};
%
\node[Box2,above=of $(GB2)!0.5!(GB3)$](GGB1){Input Data};
%
\node[Box,below=of $(B2)!0.5!(B3)$](DB1){Gradients GPU N};
\node[Box,below=of DB1](DB2){Gradient Aggregation};
\node[Box,below=of DB2](DB3){Model Update};
%
\draw[-latex](GGB1)
-|node[Text,pos=0.8]{Split into\\Non-Overlapping Subsets}(GB1);
\draw[-latex](GGB1)
-|node[Text,pos=0.8]{Split into\\Non-Overlapping Subsets}(GB2);
\draw[-latex](GGB1)
-|node[Text,pos=0.8]{Split into\\Non-Overlapping Subsets}(GB3);
\draw[-latex](GGB1)
-|node[Text,pos=0.8]{Split into\\Non-Overlapping Subsets}(GB4);
%%
\draw[-latex](GB1)--node[Text,pos=0.5]{Assigned \\to GPU 1}(B1);
\draw[-latex](GB2)--node[Text,pos=0.5]{Assigned \\to GPU 2}(B2);
\draw[-latex](GB3)--node[Text,pos=0.5]{Assigned \\to GPU 3}(B3);
\draw[-latex](GB4)--node[Text,pos=0.5]{Assigned \\to GPU 4}(B4);
%
\draw[-latex](B1)
|-node[Text,pos=0.2]{Compute\\ Gradients}(DB1);
\draw[-latex](B2)
|-node[Text,pos=0.2]{Compute\\ Gradients}(DB1);
\draw[-latex](B3)
|-node[Text,pos=0.2]{Compute\\ Gradients}(DB1);
\draw[-latex](B4)
|-node[Text,pos=0.2]{Compute\\ Gradients}(DB1);
%
\draw[-latex](DB1)--node[Text,pos=0.5]{Synchronize Gradients}(DB2);
\draw[-latex](DB2)--node[Text,pos=0.5]{Aggregate Gradients and \\Update Parameters}(DB3);
%
\draw[-latex](GGB1.east)--++(0:7)
|-node[Text,pos=0.8]{Next Mini-Batch}(DB3.east);
\end{tikzpicture}Step 1: Splitting the Dataset
The first step in data parallelism involves dividing the dataset into smaller, non-overlapping subsets. This ensures that each device processes a unique portion of the data, avoiding redundancy and enabling efficient utilization of available hardware. For instance, with a dataset of 100,000 training examples and 4 GPUs, each GPU would be assigned 25,000 examples. Modern frameworks like PyTorch’s DistributedSampler handle this distribution automatically, implementing prefetching and caching mechanisms to ensure data is readily available for processing.
Step 2: Forward Pass on Each Device
Once the data subsets are distributed, each device performs the forward pass independently. During this stage, the model processes its assigned batch of data, generating predictions and calculating the loss. For example, in a ResNet-50 model, each GPU would independently compute the convolutions, activations, and final loss for its batch. The forward pass is computationally intensive and benefits from hardware accelerators like NVIDIA V100 GPUs or Google TPUs, which are optimized for matrix operations.
Step 3: Backward Pass and Gradient Calculation
Following the forward pass, each device computes the gradients of the loss with respect to the model’s parameters during the backward pass. Modern frameworks like PyTorch and TensorFlow handle this automatically through their autograd systems. For instance, if a model has 50 million parameters, each device calculates gradients for all parameters but based only on its local data subset.
Step 4: Gradient Synchronization Across Devices
To maintain consistency across the distributed system, the gradients computed by each device must be synchronized. This step typically uses the ring all-reduce algorithm, where each GPU communicates only with its neighbors, reducing communication overhead. For example, with 8 GPUs, each sharing gradients for a 100MB model, ring all-reduce requires only 7 communication steps instead of the 56 steps needed for naive peer-to-peer synchronization.
Step 5: Updating Model Parameters
After the gradients are aggregated, the model parameters are updated using the chosen optimization algorithm (e.g., stochastic gradient descent with momentum). In frameworks like PyTorch DDP (DistributedDataParallel), these updates occur independently on each device after gradient synchronization, eliminating the need for a central parameter server.
This process—splitting data, performing computations, synchronizing results, and updating parameters—repeats for each batch of data. Modern frameworks automate this cycle, allowing developers to focus on model architecture and hyperparameter tuning rather than distributed computing logistics.
Benefits
Data parallelism offers several key benefits that make it the predominant approach for distributed training. By splitting the dataset across multiple devices and allowing each device to train an identical copy of the model, this approach effectively addresses the core challenges in modern AI training systems.
The primary advantage of data parallelism is its linear scaling capability with large datasets. As datasets grow into the terabyte range, processing them on a single machine becomes prohibitively time-consuming. For example, training a vision transformer on ImageNet (1.2 million images) might take weeks on a single GPU, but only days when distributed across 8 GPUs. This scalability is particularly valuable in domains like language modeling, where datasets can exceed billions of tokens.
Hardware utilization efficiency represents another crucial benefit. Data parallelism maintains high GPU utilization rates—typically above 85%—by ensuring each device actively processes its data portion. Modern implementations achieve this through asynchronous data loading and gradient computation overlapping with communication. For instance, while one batch computes gradients, the next batch’s data is already being loaded and preprocessed.
Implementation simplicity sets data parallelism apart from other distribution strategies. Modern frameworks have reduced complex distributed training to just a few lines of code. For example, converting a PyTorch model to use data parallelism often requires only wrapping it in DistributedDataParallel and initializing a distributed environment. This accessibility has contributed significantly to its widespread adoption in both research and industry.
The approach also offers remarkable flexibility across model architectures. Whether training a ResNet (vision), BERT (language), or Graph Neural Network (graph data), the same data parallelism principles apply without modification. This universality makes it particularly valuable as a default choice for distributed training.
Training time reduction is perhaps the most immediate benefit. Given proper implementation, data parallelism can achieve near-linear speedup with additional devices. Training that takes 100 hours on a single GPU might complete in roughly 13 hours on 8 GPUs, assuming efficient gradient synchronization and minimal communication overhead.
While these benefits make data parallelism compelling, it’s important to note that achieving these advantages requires careful system design. The next section examines the challenges that must be addressed to fully realize these benefits.
Challenges
While data parallelism is a powerful approach for distributed training, it introduces several challenges that must be addressed to achieve efficient and scalable training systems. These challenges stem from the inherent trade-offs between computation and communication, as well as the limitations imposed by hardware and network infrastructures.
Communication overhead represents the most significant bottleneck in data parallelism. During gradient synchronization, each device must exchange gradient updates—often hundreds of megabytes per step for large models. With 8 GPUs training a 1-billion-parameter model, each synchronization step might require transferring several gigabytes of data across the network. While high-speed interconnects like NVLink (300 GB/s) or InfiniBand (200 Gb/s) help, the overhead remains substantial. NCCL’s ring-allreduce5 algorithm reduces this burden by organizing devices in a ring topology, but communication costs still grow with model size and device count.
5 A communication strategy that minimizes data transfer overhead by organizing devices in a ring topology, first introduced for distributed machine learning in Horovod.
Scalability limitations become apparent as device count increases. While 8 GPUs might achieve \(7\times\) speedup (87.5% scaling efficiency), scaling to 64 GPUs typically yields only 45-50\(\times\) speedup (70-78% efficiency) due to growing synchronization costs. This non-linear scaling means that doubling the number of devices rarely halves the training time, particularly in configurations exceeding 16-32 devices.
Memory constraints present a hard limit for data parallelism. Consider a transformer model with 175 billion parameters—it requires approximately 350 GB just to store model parameters in FP32. When accounting for optimizer states and activation memories, the total requirement often exceeds 1 TB per device. Since even high-end GPUs typically offer 80GB or less, such models cannot use pure data parallelism.
Workload imbalance affects heterogeneous systems significantly. In a cluster mixing A100 and V100 GPUs, the A100s might process batches \(1.7\times\) faster, forcing them to wait for the V100s to catch up. This idle time can reduce cluster utilization by 20-30% without proper load balancing mechanisms.
Finally, there are challenges related to implementation complexity in distributed systems. While modern frameworks abstract much of the complexity, implementing data parallelism at scale still requires significant engineering effort. Ensuring fault tolerance, debugging synchronization issues, and optimizing data pipelines are non-trivial tasks that demand expertise in both machine learning and distributed systems.
Despite these challenges, data parallelism remains an important technique for distributed training, with many strategies available to address its limitations. In the next section, we will explore model parallelism, another strategy for scaling training that is particularly well-suited for handling extremely large models that cannot fit on a single device.
8.6.2 Model Parallelism
Model parallelism splits neural networks across multiple computing devices when the model’s parameters exceed single-device memory limits. Unlike data parallelism, where each device contains a complete model copy, model parallelism assigns different model components to different devices (Shazeer et al. 2017).
Shazeer, Noam, Azalia Mirhoseini, Krzysztof Maziarz, Andy Davis, Quoc Le, Geoffrey Hinton, and Jeff Dean. 2017. “Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer.” arXiv Preprint arXiv:1701.06538, January. http://arxiv.org/abs/1701.06538v1.
Several implementations of model parallelism exist. In layer-based splitting, devices process distinct groups of layers sequentially. For instance, the first device might compute layers 1-4 while the second handles layers 5-8. Channel-based splitting divides the channels within each layer across devices, such as the first device processing 512 channels while the second manages the remaining ones. For transformer architectures, attention head splitting distributes different attention heads to separate devices.
This distribution method enables training of large-scale models. GPT-3, with 175 billion parameters, relies on model parallelism for training. Vision transformers processing high-resolution 16k \(\times\) 16k pixel images use model parallelism to manage memory constraints. Mixture-of-Expert architectures leverage this approach to distribute their conditional computation paths across hardware.
Device coordination follows a specific pattern during training. In the forward pass, data flows sequentially through model segments on different devices. The backward pass propagates gradients in reverse order through these segments. During parameter updates, each device modifies only its assigned portion of the model. This coordination ensures mathematical equivalence to training on a single device while enabling the handling of models that exceed individual device memory capacities.
Mechanics
Model parallelism divides neural networks across multiple computing devices, with each device computing a distinct portion of the model’s operations. This division allows training of models whose parameter counts exceed single-device memory capacity. The technique encompasses device coordination, data flow management, and gradient computation across distributed model segments. The mechanics of model parallelism are illustrated in Figure 8.12. These steps are described next:
\begin{tikzpicture}[font=\small\sf,node distance=17mm]
\definecolor{col4}{RGB}{240,240,255}
\definecolor{col7}{RGB}{158,122,230}
\tikzset{
Box/.style={inner xsep=2pt,
draw=col7, line width=0.75pt,
fill=col4!80,
anchor=west,
text width=27mm,align=flush center,
minimum width=27mm, minimum height=10mm
},
}
\tikzset{
Text/.style={inner xsep=2pt,
draw=none, line width=0.75pt,
fill=black!07,
font=\footnotesize\sf,
align=flush center,
minimum width=22mm, minimum height=9mm
},
}
\node[Box](B1){Input Data};
\node[Box,right=of B1](B2){Model Part 1\\ on Device 1};
\node[Box,right=of B2](B3){Model Part 2\ on Device 2};
\node[Box,right=of B3](B4){Model Part 3\\ on Device 3};
\node[Box,right=of B4](B5){Predictions};
%
\draw[-latex](B1)--++(90:12mm)
-|node[Text,pos=0.25]{Forward\\ Pass}(B2.120);
\draw[latex-](B1)--++(270:12mm)
-|node[Text,pos=0.25]{Gradient\\ Updates}(B2.240);
%
\draw[-latex](B2)--++(90:12mm)
-|node[Text,pos=0.25]{Intermediate\\ Data}(B3.120);
\draw[latex-](B2)--++(270:12mm)
-|node[Text,pos=0.25]{Gradient\\ Updates}(B3.240);
%
\draw[-latex](B3)--++(90:12mm)
-|node[Text,pos=0.25]{Intermediate\\ Data}(B4.120);
\draw[latex-](B3)--++(270:12mm)
-|node[Text,pos=0.25]{Gradient\\ Updates}(B4.240);
%
\draw[-latex](B4)--++(90:12mm)
-|node[Text,pos=0.25]{Output}(B5.120);
\draw[latex-](B4)--++(270:12mm)
-|node[Text,pos=0.25]{Backward\\ Pass}(B5.240);
\end{tikzpicture}Step 1: Partitioning the Model
The first step in model parallelism is dividing the model into smaller segments. For instance, in a deep neural network, layers are often divided among devices. In a system with two GPUs, the first half of the layers might reside on GPU 1, while the second half resides on GPU 2. Another approach is to split computations within a single layer, such as dividing matrix multiplications in transformer models across devices.
Step 2: Forward Pass Through the Model
During the forward pass, data flows sequentially through the partitions. For example, data processed by the first set of layers on GPU 1 is sent to GPU 2 for processing by the next set of layers. This sequential flow ensures that the entire model is used, even though it is distributed across multiple devices. Efficient inter-device communication is crucial to minimize delays during this step (Research 2021).
Research, Microsoft. 2021. DeepSpeed: Extreme-Scale Model Training for Everyone.
Step 3: Backward Pass and Gradient Calculation
The backward pass computes gradients through the distributed model segments in reverse order. Each device calculates local gradients for its parameters and propagates necessary gradient information to previous devices. In transformer models, this means backpropagating through attention computations and feed-forward networks across device boundaries.
For example, in a two-device setup with attention mechanisms split between devices, the backward computation works as follows: The second device computes gradients for the final feed-forward layers and attention heads. It then sends the gradient tensors for the attention output to the first device. The first device uses these received gradients to compute updates for its attention parameters and earlier layer weights.
Step 4: Parameter Updates
Parameter updates occur independently on each device using the computed gradients and an optimization algorithm. A device holding attention layer parameters applies updates using only the gradients computed for those specific parameters. This localized update approach differs from data parallelism, which requires gradient averaging across devices.
The optimization step proceeds as follows: Each device applies its chosen optimizer (such as Adam or AdaFactor) to update its portion of the model parameters. A device holding the first six transformer layers updates only those layers’ weights and biases. This local parameter update eliminates the need for cross-device synchronization during the optimization step, reducing communication overhead.
Iterative Process
Like other training strategies, model parallelism repeats these steps for every batch of data. As the dataset is processed over multiple iterations, the distributed model converges toward optimal performance.
Variations of Model Parallelism
Model parallelism can be implemented through different strategies for dividing the model across devices. The three primary approaches are layer-wise partitioning, operator-level partitioning, and pipeline parallelism, each suited to different model structures and computational needs.
Layer-wise Partitioning
Layer-wise partitioning assigns distinct model layers to separate computing devices. In transformer architectures, this translates to specific devices managing defined sets of attention and feed-forward blocks. As illustrated in Figure 8.13, a 24-layer transformer model distributed across four devices assigns six consecutive transformer blocks to each device. Device 1 processes blocks 1-6, device 2 handles blocks 7-12, and so forth.
flowchart LR
subgraph Device 1
A1[<i class="fas fa-cube"></i> Blocks 1-6]
B1[<i class="fas fa-microchip"></i> GPU 1]
end
subgraph Device 2
A2[<i class="fas fa-cube"></i> Blocks 7-12]
B2[<i class="fas fa-microchip"></i> GPU 2]
end
subgraph Device 3
A3[<i class="fas fa-cube"></i> Blocks 13-18]
B3[<i class="fas fa-microchip"></i> GPU 3]
end
subgraph Device 4
A4[<i class="fas fa-cube"></i> Blocks 19-24]
B4[<i class="fas fa-microchip"></i> GPU 4]
end
A1 --> A2
A2 --> A3
A3 --> A4
A4 --> A3
A3 --> A2
A2 --> A1
%% Defining the styles
classDef Red fill:#FF9999;
classDef Amber fill:#FFDEAD;
classDef Green fill:#BDFFA4;
classDef Blue fill:#99CCFF;
%% Assigning styles to nodes
class A1 Red;
class A2 Amber;
class A3 Green;
class A4 Blue;
This sequential processing introduces device idle time, as each device must wait for the previous device to complete its computation before beginning work. For example, while device 1 processes the initial blocks, devices 2, 3, and 4 remain inactive. Similarly, when device 2 begins its computation, device 1 sits idle. This pattern of waiting and idle time reduces hardware utilization efficiency compared to other parallelization strategies.
Layer-wise partitioning assigns distinct model layers to separate computing devices. In transformer architectures, this translates to specific devices managing defined sets of attention and feed-forward blocks. A 24-layer transformer model distributed across four devices assigns six consecutive transformer blocks to each device. Device 1 processes blocks 1-6, device 2 handles blocks 7-12, and so forth.
Pipeline Parallelism
Pipeline parallelism extends layer-wise partitioning by introducing microbatching to minimize device idle time, as illustrated in Figure 8.14. Instead of waiting for an entire batch to sequentially pass through all devices, the computation is divided into smaller segments called microbatches [harlap2018pipedream]. Each device, as represented by the rows in the drawing, processes its assigned model layers for different microbatches simultaneously. For example, the forward pass involves devices passing activations to the next stage (e.g., \(F_{0,0}\) to \(F_{1,0}\)). The backward pass transfers gradients back through the pipeline (e.g., \(B_{3,3}\) to \(B_{2,3}\)). This overlapping computation reduces idle time and increases throughput while maintaining the logical sequence of operations across devices.
\begin{tikzpicture}[
every node/.style={font=\sffamily, draw, minimum width=1cm, minimum height=0.7cm, align=center, outer sep=0},
fill0/.style={fill=red!20}, % Complementary to lightgray
fill1/.style={fill=blue!20}, % Complementary to orange
fill2/.style={fill=orange!20}, % Complementary to blue
fill3/.style={fill=yellow!20}, % Complementary to purple
back3/.style={fill=yellow!20} % Same as fill3
]
% Row 0
\node[fill0] (F0_0) {$F_{0,0}$};
\node[fill0, right=0cm of F0_0] (F0_1) {$F_{0,1}$};
\node[fill0, right=0cm of F0_1] (F0_2) {$F_{0,2}$};
\node[fill0, right=0cm of F0_2] (F0_3) {$F_{0,3}$};
% Row 1
\node[fill1, above right=0cm and 0cm of F0_0] (F1_0) {$F_{1,0}$};
\node[fill1, right=0cm of F1_0] (F1_1) {$F_{1,1}$};
\node[fill1, right=0cm of F1_1] (F1_2) {$F_{1,2}$};
\node[fill1, right=0cm of F1_2] (F1_3) {$F_{1,3}$};
% Row 2 (stacked above F1)
\node[fill2, above right=0cm and 0cm of F1_0] (F2_0) {$F_{2,0}$};
\node[fill2, right=0cm of F2_0] (F2_1) {$F_{2,1}$};
\node[fill2, right=0cm of F2_1] (F2_2) {$F_{2,2}$};
\node[fill2, right=0cm of F2_2] (F2_3) {$F_{2,3}$};
% Row 3 (stacked above F2)
\node[fill3, above right=0cm and 0cm of F2_0] (F3_0) {$F_{3,0}$};
\node[fill3, right=0cm of F3_0] (F3_1) {$F_{3,1}$};
\node[fill3, right=0cm of F3_1] (F3_2) {$F_{3,2}$};
\node[fill3, right=0cm of F3_2] (F3_3) {$F_{3,3}$};
% Row 3 (backward pass)
\node[back3, right=0cm of F3_3] (B3_3) {$B_{3,3}$};
\node[back3, right=0cm of B3_3] (B3_2) {$B_{3,2}$};
\node[back3, right=0cm of B3_2] (B3_1) {$B_{3,1}$};
\node[back3, right=0cm of B3_1] (B3_0) {$B_{3,0}$};
% Row 2 (backward pass)
\node[fill2, below=0cm and 0cm of B3_2] (B2_3) {$B_{2,3}$};
\node[fill2, right=0cm of B2_3] (B2_2) {$B_{2,2}$};
\node[fill2, right=0cm of B2_2] (B2_1) {$B_{2,1}$};
\node[fill2, right=0cm of B2_1] (B2_0) {$B_{2,0}$};
% Row 1 (backward pass)
\node[fill1, below=0cm of B2_2] (B1_3) {$B_{1,3}$};
\node[fill1, right=0cm of B1_3] (B1_2) {$B_{1,2}$};
\node[fill1, right=0cm of B1_2] (B1_1) {$B_{1,1}$};
\node[fill1, right=0cm of B1_1] (B1_0) {$B_{1,0}$};
% Row 0 (backward pass)
\node[fill0, below=0cm of B1_2] (B0_3) {$B_{0,3}$};
\node[fill0, right=0cm of B0_3] (B0_2) {$B_{0,2}$};
\node[fill0, right=0cm of B0_2] (B0_1) {$B_{0,1}$};
\node[fill0, right=0cm of B0_1] (B0_0) {$B_{0,0}$};
% Update nodes
\node[fill0, right=0cm of B0_0] (U0_0) {Update};
\node[fill1, above=0cm of U0_0] (U0_1) {Update};
\node[fill2, above=0cm of U0_1] (U0_2) {Update};
\node[fill3, above=0cm of U0_2] (U0_3) {Update};
%\node[draw=none, minimum width=4cm, minimum height=1cm, align=center, right=1cm of F0_3] (Bubble) {Bubble};
\end{tikzpicture}In a transformer model distributed across four devices, device 1 would process blocks 1-6 for microbatch \(N+1\) while device 2 computes blocks 7-12 for microbatch \(N\). Simultaneously, device 3 executes blocks 13-18 for microbatch \(N-1\), and device 4 processes blocks 19-24 for microbatch \(N-2\). Each device maintains its assigned transformer blocks but operates on a different microbatch, creating a continuous flow of computation.
The transfer of hidden states between devices occurs continuously rather than in distinct phases. When device 1 completes processing a microbatch, it immediately transfers the output tensor of shape [microbatch_size, sequence_length, hidden_dimension] to device 2 and begins processing the next microbatch. This overlapping computation pattern maintains full hardware utilization while preserving the model’s mathematical properties.
Operator-level Parallelism
Operator-level parallelism divides individual neural network operations across devices. In transformer models, this often means splitting attention computations. Consider a transformer with 64 attention heads and a hidden dimension of 4096. Two devices might split this computation as follows: Device 1 processes attention heads 1-32, computing queries, keys, and values for its assigned heads. Device 2 simultaneously processes heads 33-64. Each device handles attention computations for [batch_size, sequence_length, 2048] dimensional tensors.
Matrix multiplication operations in feed-forward networks also benefit from operator-level splitting. A feed-forward layer with input dimension 4096 and intermediate dimension 16384 can split across devices along the intermediate dimension. Device 1 computes the first 8192 intermediate features, while device 2 computes the remaining 8192 features. This division reduces peak memory usage while maintaining mathematical equivalence to the original computation.
Summary
Each of these partitioning methods addresses specific challenges in training large models, and their applicability depends on the model architecture and the resources available. By selecting the appropriate strategy, practitioners can train models that exceed the limits of individual devices, enabling the development of cutting-edge machine learning systems.
8.6.3 Benefits
Model parallelism offers several significant benefits, making it an essential strategy for training large-scale models that exceed the capacity of individual devices. These advantages stem from its ability to partition the workload across multiple devices, enabling the training of more complex and resource-intensive architectures.
Memory scaling represents the primary advantage of model parallelism. Current transformer architectures contain up to hundreds of billions of parameters. A 175 billion parameter model with 32-bit floating point precision requires 700 GB of memory just to store its parameters. When accounting for activations, optimizer states, and gradients during training, the memory requirement multiplies several fold. Model parallelism makes training such architectures feasible by distributing these memory requirements across devices.
Another key advantage is the efficient utilization of device memory and compute power. Since each device only needs to store and process a portion of the model, memory usage is distributed across the system. This allows practitioners to work with larger batch sizes or more complex layers without exceeding memory limits, which can also improve training stability and convergence.
Model parallelism also provides flexibility for different model architectures. Whether the model is sequential, as in many natural language processing tasks, or composed of computationally intensive operations, as in attention-based models or convolutional networks, there is a partitioning strategy that fits the architecture. This adaptability makes model parallelism applicable to a wide variety of tasks and domains.
Finally, model parallelism is a natural complement to other distributed training strategies, such as data parallelism and pipeline parallelism. By combining these approaches, it becomes possible to train models that are both large in size and require extensive data. This hybrid flexibility is especially valuable in cutting-edge research and production environments, where scaling models and datasets simultaneously is critical for achieving state-of-the-art performance.
While model parallelism introduces these benefits, its effectiveness depends on the careful design and implementation of the partitioning strategy. In the next section, we will discuss the challenges associated with model parallelism and the trade-offs involved in its use.
8.6.4 Challenges
While model parallelism provides a powerful approach for training large-scale models, it also introduces unique challenges. These challenges arise from the complexity of partitioning the model and the dependencies between partitions during training. Addressing these issues requires careful system design and optimization.
One major challenge in model parallelism is balancing the workload across devices. Not all parts of a model require the same amount of computation. For instance, in layer-wise partitioning, some layers may perform significantly more operations than others, leading to an uneven distribution of work. Devices responsible for the heavier computations may become bottlenecks, leaving others underutilized. This imbalance reduces overall efficiency and slows down training. Identifying optimal partitioning strategies is critical to ensuring all devices contribute evenly.
Another challenge is data dependency between devices. During the forward pass, activation tensors of shape [batch_size, sequence_length, hidden_dimension] must transfer between devices. For a typical transformer model with batch size 32, sequence length 2048, and hidden dimension 2048, each transfer moves approximately 512 MB of data at float32 precision. With gradient transfers in the backward pass, a single training step can require several gigabytes of inter-device communication. On systems using PCIe interconnects with 64 GB/s theoretical bandwidth, these transfers introduce significant latency.
Model parallelism also increases the complexity of implementation and debugging. Partitioning the model, ensuring proper data flow, and synchronizing gradients across devices require detailed coordination. Errors in any of these steps can lead to incorrect gradient updates or even model divergence. Debugging such errors is often more difficult in distributed systems, as issues may arise only under specific conditions or workloads.
A further challenge is pipeline bubbles in pipeline parallelism. With m pipeline stages, the first \(m-1\) steps operate at reduced efficiency as the pipeline fills. For example, in an 8-device pipeline, the first device begins processing immediately, but the eighth device remains idle for 7 steps. This warmup period reduces hardware utilization by approximately \((m-1)/b\) percent, where \(b\) is the number of batches in the training step.
Finally, model parallelism may be less effective for certain architectures, such as models with highly interdependent operations. In these cases, splitting the model may lead to excessive communication overhead, outweighing the benefits of parallel computation. For such models, alternative strategies like data parallelism or hybrid approaches might be more suitable.
Despite these challenges, model parallelism remains an indispensable tool for training large models. With careful optimization and the use of modern frameworks, many of these issues can be mitigated, enabling efficient distributed training at scale.
8.6.5 Hybrid Parallelism
Hybrid parallelism combines model parallelism and data parallelism when training neural networks (Narayanan et al. 2021). A model might be too large to store on one GPU (requiring model parallelism) while simultaneously needing to process large batches of data efficiently (requiring data parallelism).
Narayanan, Deepak, Mohammad Shoeybi, Jared Casper, Patrick LeGresley, Mostofa Patwary, Vijay Korthikanti, Dmitri Vainbrand, et al. 2021. “Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM.” In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, 1–15. ACM. https://doi.org/10.1145/3458817.3476209.
Training a 175-billion parameter language model on a dataset of 300 billion tokens demonstrates hybrid parallelism in practice. The neural network layers distribute across multiple GPUs through model parallelism, while data parallelism enables different GPU groups to process separate batches. The hybrid approach coordinates these two forms of parallelization.
This strategy addresses two fundamental constraints. First, memory constraints arise when model parameters exceed single-device memory capacity. Second, computational demands increase when dataset size necessitates distributed processing.
Mechanics
Hybrid parallelism operates by combining the processes of model partitioning and dataset splitting, ensuring efficient utilization of both memory and computation across devices. This integration allows large-scale machine learning systems to overcome the constraints imposed by individual parallelism strategies.
Partitioning Model and Data
Hybrid parallelism divides both model architecture and training data across devices. The model divides through layer-wise or operator-level partitioning, where GPUs process distinct neural network segments. Simultaneously, the dataset splits into subsets, allowing each device group to train on different batches. A transformer model might distribute its attention layers across four GPUs, while each GPU group processes a unique 1,000-example batch. This dual partitioning distributes memory requirements and computational workload.
Forward Pass
During the forward pass, input data flows through the distributed model. Each device processes its assigned portion of the model using the data subset it holds. For example, in a hybrid system with four devices, two devices might handle different layers of the model (model parallelism) while simultaneously processing distinct data batches (data parallelism). Communication between devices ensures that intermediate outputs from model partitions are passed seamlessly to subsequent partitions.
Backward Pass and Gradient Calculation
During the backward pass, gradients are calculated for the model partitions stored on each device. Data-parallel devices that process the same subset of the model but different data batches aggregate their gradients, ensuring that updates reflect contributions from the entire dataset. For model-parallel devices, gradients are computed locally and passed to the next layer in reverse order. In a two-device model-parallel configuration, for example, the first device computes gradients for layers 1-3, then transmits these to the second device for layers 4-6. This combination of gradient synchronization and inter-device communication ensures consistency across the distributed system.
Parameter Updates
After gradient synchronization, model parameters are updated using the chosen optimization algorithm. Devices working in data parallelism update their shared model partitions consistently, while model-parallel devices apply updates to their local segments. Efficient communication is critical in this step to minimize delays and ensure that updates are correctly propagated across all devices.
Iterative Process
Hybrid parallelism follows an iterative process similar to other training strategies. The combination of model and data distribution allows the system to process large datasets and complex models efficiently over multiple training epochs. By balancing the computational workload and memory requirements, hybrid parallelism enables the training of advanced machine learning models that would otherwise be infeasible.
Variations of Hybrid Parallelism
Hybrid parallelism can be implemented in different configurations, depending on the model architecture, dataset characteristics, and available hardware. These variations allow for tailored solutions that optimize performance and scalability for specific training requirements.
Hierarchical Hybrid Parallelism
Hierarchical hybrid parallelism applies model parallelism to divide the model across devices first and then layers data parallelism on top to handle the dataset distribution. For example, in a system with eight devices, four devices may hold different partitions of the model, while each partition is replicated across the other four devices for data parallel processing. This approach is well-suited for large models with billions of parameters, where memory constraints are a primary concern.
Hierarchical hybrid parallelism ensures that the model size is distributed across devices, reducing memory requirements, while data parallelism ensures that multiple data samples are processed simultaneously, improving throughput. This dual-layered approach is particularly effective for models like transformers, where each layer may have a significant memory footprint.
Intra-layer Hybrid Parallelism
Intra-layer hybrid parallelism combines model and data parallelism within individual layers of the model. For instance, in a transformer architecture, the attention mechanism can be split across multiple devices (model parallelism), while each device processes distinct batches of data (data parallelism). This fine-grained integration allows the system to optimize resource usage at the level of individual operations, enabling training for models with extremely large intermediate computations.
This variation is particularly useful in scenarios where specific layers, such as attention or feedforward layers, have computationally intensive operations that are difficult to distribute effectively using model or data parallelism alone. Intra-layer hybrid parallelism addresses this challenge by applying both strategies simultaneously.
Inter-layer Hybrid Parallelism
Inter-layer hybrid parallelism focuses on distributing the workload between model and data parallelism at the level of distinct model layers. For example, early layers of a neural network may be distributed using model parallelism, while later layers leverage data parallelism. This approach aligns with the observation that certain layers in a model may be more memory-intensive, while others benefit from increased data throughput.
This configuration allows for dynamic allocation of resources, adapting to the specific demands of different layers in the model. By tailoring the parallelism strategy to the unique characteristics of each layer, inter-layer hybrid parallelism achieves an optimal balance between memory usage and computational efficiency.
Benefits
The adoption of hybrid parallelism in machine learning systems addresses some of the most significant challenges posed by the ever-growing scale of models and datasets. By blending the strengths of model parallelism and data parallelism, this approach provides a comprehensive solution to scaling modern machine learning workloads.
One of the most prominent benefits of hybrid parallelism is its ability to scale seamlessly across both the model and the dataset. Modern neural networks, particularly transformers used in natural language processing and vision applications, often contain billions of parameters. These models, paired with massive datasets, make training on a single device impractical or even impossible. Hybrid parallelism enables the division of the model across multiple devices to manage memory constraints while simultaneously distributing the dataset to process vast amounts of data efficiently. This dual capability ensures that training systems can handle the computational and memory demands of the largest models and datasets without compromise.
Another critical advantage lies in hardware utilization. In many distributed training systems, inefficiencies can arise when devices sit idle during different stages of computation or synchronization. Hybrid parallelism mitigates this issue by ensuring that all devices are actively engaged. Whether a device is computing forward passes through its portion of the model or processing data batches, hybrid strategies maximize resource usage, leading to faster training times and improved throughput.
Flexibility is another hallmark of hybrid parallelism. Machine learning models vary widely in architecture and computational demands. For instance, convolutional neural networks prioritize spatial data processing, while transformers require intensive operations like matrix multiplications in attention mechanisms. Hybrid parallelism adapts to these diverse needs by allowing practitioners to apply model and data parallelism selectively. This adaptability ensures that hybrid approaches can be tailored to the specific requirements of a given model, making it a versatile solution for diverse training scenarios.
Moreover, hybrid parallelism reduces communication bottlenecks, a common issue in distributed systems. By striking a balance between distributing model computations and spreading data processing, hybrid strategies minimize the amount of inter-device communication required during training. This efficient coordination not only speeds up the training process but also enables the effective use of large-scale distributed systems where network latency might otherwise limit performance.
Finally, hybrid parallelism supports the ambitious scale of modern AI research and development. It provides a framework for leveraging cutting-edge hardware infrastructures, including clusters of GPUs or TPUs, to train models that push the boundaries of what’s possible. Without hybrid parallelism, many of the breakthroughs in AI—such as large language models or advanced vision systems—would remain unattainable due to resource limitations.
By enabling scalability, maximizing hardware efficiency, and offering flexibility, hybrid parallelism has become an essential strategy for training the most complex machine learning systems. It is not just a solution to today’s challenges but also a foundation for the future of AI, where models and datasets will continue to grow in complexity and size.
Challenges
While hybrid parallelism provides a robust framework for scaling machine learning training, it also introduces complexities that require careful consideration. These challenges stem from the intricate coordination needed to integrate both model and data parallelism effectively. Understanding these obstacles is crucial for designing efficient hybrid systems and avoiding potential bottlenecks.
One of the primary challenges of hybrid parallelism is communication overhead. Both model and data parallelism involve significant inter-device communication. In model parallelism, devices must exchange intermediate outputs and gradients to maintain the sequential flow of computation. In data parallelism, gradients computed on separate data subsets must be synchronized across devices. Hybrid parallelism compounds these demands, as it requires efficient communication for both processes simultaneously. If not managed properly, the resulting overhead can negate the benefits of parallelization, particularly in large-scale systems with slower interconnects or high network latency.
Another critical challenge is the complexity of implementation. Hybrid parallelism demands a nuanced understanding of both model and data parallelism techniques, as well as the underlying hardware and software infrastructure. Designing efficient hybrid strategies involves making decisions about how to partition the model, how to distribute data, and how to synchronize computations across devices. This process often requires extensive experimentation and optimization, particularly for custom architectures or non-standard hardware setups. While modern frameworks like PyTorch and TensorFlow provide tools for distributed training, implementing hybrid parallelism at scale still requires significant engineering expertise.
Workload balancing also presents a challenge in hybrid parallelism. In a distributed system, not all devices may have equal computational capacity. Some devices may process data or compute gradients faster than others, leading to inefficiencies as faster devices wait for slower ones to complete their tasks. Additionally, certain model layers or operations may require more resources than others, creating imbalances in computational load. Managing this disparity requires careful tuning of partitioning strategies and the use of dynamic workload distribution techniques.
Memory constraints remain a concern, even in hybrid setups. While model parallelism addresses the issue of fitting large models into device memory, the additional memory requirements for data parallelism, such as storing multiple data batches and gradient buffers, can still exceed available capacity. This is especially true for models with extremely large intermediate computations, such as transformers with high-dimensional attention mechanisms. Balancing memory usage across devices is essential to prevent resource exhaustion during training.
Lastly, hybrid parallelism poses challenges related to fault tolerance and debugging. Distributed systems are inherently more prone to hardware failures and synchronization errors. Debugging issues in hybrid setups can be significantly more complex than in standalone model or data parallelism systems, as errors may arise from interactions between the two approaches. Ensuring robust fault-tolerance mechanisms and designing tools for monitoring and debugging distributed systems are essential for maintaining reliability.
Despite these challenges, hybrid parallelism remains an indispensable strategy for training state-of-the-art machine learning models. By addressing these obstacles through optimized communication protocols, intelligent partitioning strategies, and robust fault-tolerance systems, practitioners can unlock the full potential of hybrid parallelism and drive innovation in AI research and applications.
8.6.6 Comparison
The features of data parallelism, model parallelism, and hybrid parallelism are summarized in Table 8.6. This comparison highlights their respective focuses, memory requirements, communication overheads, scalability, implementation complexity, and ideal use cases. By examining these factors, practitioners can determine the most suitable approach for their training needs.
| Aspect | Data Parallelism | Model Parallelism | Hybrid Parallelism |
|---|---|---|---|
| Focus | Distributes dataset across devices, each with a full model copy | Distributes the model across devices, each handling a portion of the model | Combines model and data parallelism for balanced scalability |
| Memory Requirement per Device | High (entire model on each device) | Low (model split across devices) | Moderate (splits model and dataset across devices) |
| Communication Overhead | Moderate to High (gradient synchronization across devices) | High (communication for intermediate activations and gradients) | Very High (requires synchronization for both model and data) |
| Scalability | Good for large datasets with moderate model sizes | Good for very large models with smaller datasets | Excellent for extremely large models and datasets |
| Implementation Complexity | Low to Moderate (relatively straightforward with existing tools) | Moderate to High (requires careful partitioning and coordination) | High (complex integration of model and data parallelism) |
| Ideal Use Case | Large datasets where model fits within a single device | Extremely large models that exceed single-device memory limits | Training massive models on vast datasets in large-scale systems |
Figure 8.15 provides a general guideline for selecting parallelism strategies in distributed training systems. While the chart offers a structured decision-making process based on model size, dataset size, and scaling constraints, it is intentionally simplified. Real-world scenarios often involve additional complexities such as hardware heterogeneity, communication bandwidth, and workload imbalance, which may influence the choice of parallelism techniques. The chart is best viewed as a foundational tool for understanding the trade-offs and decision points in parallelism strategy selection. Practitioners should consider this guideline as a starting point and adapt it to the specific requirements and constraints of their systems to achieve optimal performance.
\begin{tikzpicture}[font=\small\sf,node distance=11mm]
\definecolor{col2}{RGB}{255, 255, 128}
\definecolor{col5}{RGB}{170,170,51}
\definecolor{col7}{RGB}{72,84,69}
\definecolor{col4}{RGB}{229,255,229}
\tikzset{
Box/.style={inner xsep=2pt,
draw=col7, line width=0.75pt,
fill=col4,
anchor=west,
text width=27mm,align=flush center,
minimum width=27mm, minimum height=10mm
},
Box1/.style={inner xsep=2pt,
draw=col7, line width=0.75pt,
fill=green!10,
anchor=west,
text width=31mm,align=flush center,
minimum width=32mm, minimum height=10mm
},
}
\tikzset{
Text/.style={inner xsep=2pt,
draw=none, line width=0.75pt,
fill=black!10,
font=\footnotesize\sf,
align=flush center,
minimum width=7mm, minimum height=5mm
},
}
\node[Box](B1){Hybrid\\ Parallelism};
\node[Box,node distance=8mm,right=of B1](B2){Model\\Parallelism};
\node[Box,node distance=8 mm,right=of B2](B3){Data\\ Parallelism};
\node[Box,right=of B3](B4){Single Device Optimization};
%
\scoped[on background layer]
\node[draw=col5,inner xsep=5mm,inner ysep=5mm,
yshift=-1mm,
fill=col2!40,fit=(B1)(B3),line width=0.75pt](BB){};
\node[above=16pt of BB.south west,
%xshift=19mm,
anchor=north west]{Parallelism Opportunities};
\node[Box,,node distance=18mm,
above=of B4](G1B4){Is the dataset\\ very large?};
\node[Box1,node distance=18mm,
above=of $(B2.north)!0.5!(B3.north)$](G1B3){Is scaling the model\\ or data more critical?};
\node[Box1,above=of G1B3](G2B3){Are both constraints significant?};
\node[Box1,above=of G2B3](G3B3){Does the dataset fit\\ in a single device?};
\node[Box1,above=of G3B3](G4B3){Does the model fit\\ in a single device?};
\node[Box,node distance=6mm,above=of G4B3](G5B3){Start};
%
\node[Box,below=of B2](DB2){End};
%
\draw[-latex](G5B3)--(G4B3);
\draw[-latex](G4B3)--node[Text]{No}(G3B3);
\draw[-latex](G4B3)-|node[Text,pos=0.1]{Yes}(G1B4);
\draw[-latex](G3B3)--node[Text,pos=0.5]{No}(G2B3);
\draw[-latex](G2B3)--node[Text,pos=0.5]{No}(G1B3);
\draw[-latex](G1B4)--node[Text,pos=0.5]{No}(B4);
%
\draw[-latex](G3B3)-|node[Text,pos=0.22]{Yes}(B2.150);
\draw[-latex](G2B3)-|node[Text,pos=0.32]{Yes}(B1);
\draw[-latex](G1B3.south)--++(270:7mm)-|node[Text,pos=0.22]{Scaling\\ Model}(B2);
\draw[-latex](G1B3.south)--++(270:7mm)-|node[Text,pos=0.22]{Scaling\\ Model}(B3);
\draw[-latex](G1B4)-|node[Text,pos=0.22]{Yes}(B3.40);
%
\draw[-latex](B1)|-(DB2);
\draw[-latex](B3)|-(DB2);
\draw[-latex](B2)--(DB2);
\end{tikzpicture}8.7 Optimization Techniques for Training Systems
Efficient training of machine learning models relies on identifying and addressing the factors that limit performance and scalability. This section explores a range of optimization techniques designed to improve the efficiency of training systems. By targeting specific bottlenecks, optimizing hardware and software interactions, and employing scalable training strategies, these methods enable practitioners to build systems that effectively utilize resources while minimizing training time.
8.7.1 Identifying Bottlenecks in Training
Effective optimization of training systems requires a systematic approach to identifying and addressing performance bottlenecks. Bottlenecks can arise at various levels, including computation, memory, and data handling, and they directly impact the efficiency and scalability of the training process.
Computational bottlenecks can significantly impact training efficiency. One common bottleneck occurs when computational resources, such as GPUs or TPUs, are underutilized. This can happen due to imbalanced workloads or inefficient parallelization strategies. For example, if one device completes its assigned computation faster than others, it remains idle while waiting for the slower devices to catch up. Such inefficiencies reduce the overall training throughput.
Memory-related bottlenecks are particularly challenging when dealing with large models. Insufficient memory can lead to frequent swapping of data between device memory and slower storage, significantly slowing down the training process. In some cases, the memory required to store intermediate activations during the forward and backward passes can exceed the available capacity, forcing the system to employ techniques such as gradient checkpointing, which trade off computational efficiency for memory savings.
Data handling bottlenecks can severely limit the utilization of computational resources. Training systems often rely on a continuous supply of data to keep computational resources fully utilized. If data loading and preprocessing are not optimized, computational devices may sit idle while waiting for new batches of data to arrive. This issue is particularly prevalent when training on large datasets stored on networked file systems or remote storage solutions.
Identifying these bottlenecks typically involves using profiling tools to analyze the performance of the training system. Tools integrated into machine learning frameworks, such as PyTorch’s torch.profiler or TensorFlow’s tf.data analysis utilities, can provide detailed insights into where time and resources are being spent during training. By pinpointing the specific stages or operations that are causing delays, practitioners can design targeted optimizations to address these issues effectively.
8.7.2 System-Level Optimizations
After identifying the bottlenecks in a training system, the next step is to implement optimizations at the system level. These optimizations target the underlying hardware, data flow, and resource allocation to improve overall performance and scalability.
One essential technique is profiling training workloads. Profiling involves collecting detailed metrics about the system’s performance during training, such as computation times, memory usage, and communication overhead. These metrics help reveal inefficiencies, such as imbalanced resource usage or excessive time spent in specific stages of the training pipeline. Profiling tools such as NVIDIA Nsight Systems or TensorFlow Profiler can provide actionable insights, enabling developers to make informed adjustments to their training configurations.
Leveraging hardware-specific features is another critical aspect of system-level optimization. Modern accelerators, such as GPUs and TPUs, include specialized capabilities that can significantly enhance performance when utilized effectively. For instance, mixed precision training, which uses lower-precision floating-point formats like FP16 or bfloat166 for computations, can dramatically reduce memory usage and improve throughput without sacrificing model accuracy. Similarly, tensor cores in NVIDIA GPUs are designed to accelerate matrix operations, a common computational workload in deep learning, making them ideal for optimizing forward and backward passes.
6 Google’s bfloat16 format retains FP32’s dynamic range while reducing precision, making it highly effective for deep learning training on TPUs.
Data pipeline optimization is also an important consideration at the system level. Ensuring that data is loaded, preprocessed, and delivered to the training devices efficiently can eliminate potential bottlenecks caused by slow data delivery. Techniques such as caching frequently used data, prefetching batches to overlap computation and data loading, and using efficient data storage formats like TFRecord or RecordIO can help maintain a steady flow of data to computational devices.
8.7.3 Software-Level Optimizations
In addition to system-level adjustments, software-level optimizations focus on improving the efficiency of training algorithms and their implementation within machine learning frameworks.
One effective software-level optimization is the use of fused kernels. In traditional implementations, operations like matrix multiplications, activation functions, and gradient calculations are often executed as separate steps. Fused kernels combine these operations into a single optimized routine, reducing the overhead associated with launching multiple operations and improving cache utilization. Many frameworks, such as PyTorch and TensorFlow, automatically apply kernel fusion where possible, but developers can further optimize custom operations by explicitly using libraries like cuBLAS or cuDNN.
Dynamic graph execution is another powerful technique for software-level optimization. In frameworks that support dynamic computation graphs, such as PyTorch, the graph of operations is constructed on-the-fly during each training iteration. This flexibility allows for fine-grained optimizations based on the specific inputs and outputs of a given iteration. Dynamic graphs also enable more efficient handling of variable-length sequences, such as those encountered in natural language processing tasks.
Gradient accumulation is an additional strategy that can be implemented at the software level to address memory constraints. Instead of updating model parameters after every batch, gradient accumulation allows the system to compute gradients over multiple smaller batches and update parameters only after aggregating them. This approach effectively increases the batch size without requiring additional memory, enabling training on larger datasets or models.
8.7.4 Scaling Techniques
Scaling techniques aim to extend the capabilities of training systems to handle larger datasets and models by optimizing the training configuration and resource allocation.
One common scaling technique is batch size scaling. Increasing the batch size can reduce the number of synchronization steps required during training, as fewer updates are needed to process the same amount of data. However, larger batch sizes may introduce challenges, such as slower convergence or reduced generalization. Techniques like learning rate scaling and warmup schedules can help mitigate these issues, ensuring stable and effective training even with large batches.
Layer-freezing strategies provide another method for scaling training systems efficiently. In many scenarios, particularly in transfer learning, the lower layers of a model capture general features and do not need frequent updates. By freezing these layers and allowing only the upper layers to train, memory and computational resources can be conserved, enabling the system to focus its efforts on fine-tuning the most critical parts of the model.
8.8 Training on Specialized Hardware
The evolution of specialized machine learning hardware represents a critical development in addressing the computational demands of modern training systems. Each hardware architecture—including GPUs, TPUs, FPGAs, and ASICs—embodies distinct design philosophies and engineering trade-offs that optimize for specific aspects of the training process. These specialized processors have fundamentally altered the scalability and efficiency constraints of machine learning systems, enabling breakthroughs in model complexity and training speed. We briefly examine the architectural principles, performance characteristics, and practical applications of each hardware type, highlighting their indispensable role in shaping the future capabilities of machine learning training systems.
8.8.1 GPUs
Machine learning training systems demand immense computational power to process large datasets, perform gradient computations, and update model parameters efficiently. GPUs have emerged as a critical technology to meet these requirements (Figure 8.17), primarily due to their highly parallelized architecture and ability to execute the dense linear algebra operations central to neural network training (Dally, Keckler, and Kirk 2021).
Dally, William J., Stephen W. Keckler, and David B. Kirk. 2021. “Evolution of the Graphics Processing Unit (GPU).” IEEE Micro 41 (6): 42–51. https://doi.org/10.1109/mm.2021.3113475.
From the perspective of training pipeline architecture, GPUs address several key bottlenecks. The large number of cores in GPUs allows for simultaneous processing of thousands of matrix multiplications, accelerating the forward and backward passes of training. In systems where data throughput limits GPU utilization, prefetching and caching mechanisms help maintain a steady flow of data. These optimizations, previously discussed in training pipeline design, are critical to unlocking the full potential of GPUs (Patterson and Hennessy 2021b).
———. 2021b. Computer Organization and Design RISC-v Edition: The Hardware Software Interface. 2nd ed. San Francisco, CA: Morgan Kaufmann.
In distributed training systems, GPUs enable scalable strategies such as data parallelism and model parallelism. NVIDIA’s ecosystem, including tools like NCCL for multi-GPU communication, facilitates efficient parameter synchronization, a frequent challenge in large-scale setups. For example, in training large models like GPT-3, GPUs were used in tandem with distributed frameworks to split computations across thousands of devices while addressing memory and compute scaling issues (Brown, Mann, Ryder, Subbiah, Kaplan, Dhariwal, et al. 2020).
Hardware-specific features further enhance GPU performance. NVIDIA’s tensor cores, for instance, are optimized for mixed-precision training, which reduces memory usage while maintaining numerical stability (Micikevicius et al. 2017b). This directly addresses memory constraints, a common bottleneck in training massive models. Combined with software-level optimizations like fused kernels, GPUs deliver substantial speedups in both single-device and multi-device configurations.
———, et al. 2017b. “Mixed Precision Training.” arXiv Preprint arXiv:1710.03740, October. http://arxiv.org/abs/1710.03740v3.
A case study that exemplifies the role of GPUs in machine learning training is OpenAI’s use of NVIDIA hardware for large language models. Training GPT-3, with its 175 billion parameters, required distributed processing across thousands of V100 GPUs. The combination of GPU-optimized frameworks, advanced communication protocols, and hardware features enabled OpenAI to achieve this ambitious scale efficiently (Brown, Mann, Ryder, Subbiah, Kaplan, Dhariwal, et al. 2020).
Despite their advantages, GPUs are not without challenges. Effective utilization of GPUs demands careful attention to workload balancing and inter-device communication. Training systems must also consider the cost implications, as GPUs are resource-intensive and require optimized data centers to operate at scale. However, with innovations like NVLink and CUDA-X libraries, these challenges are continually being addressed.
In conclusion, GPUs are indispensable for modern machine learning training systems due to their versatility, scalability, and integration with advanced software frameworks. By addressing key bottlenecks in computation, memory, and distribution, GPUs play a foundational role in enabling the large-scale training pipelines discussed throughout this chapter.
8.8.2 TPUs
Tensor Processing Units (TPUs) and other custom accelerators have been purpose-built to address the unique challenges of large-scale machine learning training. Unlike GPUs, which are versatile and serve a wide range of applications, TPUs are specifically optimized for the computational patterns found in deep learning, such as matrix multiplications and convolutional operations (Jouppi et al. 2017b). These devices address several bottlenecks in training pipelines by offering high throughput, specialized memory handling, and tight integration with specific machine learning frameworks.
TPUs were developed by Google with a primary goal: to accelerate machine learning workloads at scale while reducing the energy and infrastructure costs associated with traditional hardware. Their architecture is optimized for tasks that benefit from batch processing, making them particularly effective in distributed training systems where large datasets are split across multiple devices. For example, TPUs leverage systolic array architectures, which perform efficient matrix multiplications by streaming data through a network of processing elements. This design reduces latency and energy consumption, a key advantage when training large-scale models like transformers (Jouppi et al. 2017b).
———, et al. 2017b. “In-Datacenter Performance Analysis of a Tensor Processing Unit.” In Proceedings of the 44th Annual International Symposium on Computer Architecture, 1–12. ACM. https://doi.org/10.1145/3079856.3080246.
Abadi, Martín, Ashish Agarwal, Paul Barham, Eugene Brevdo, Zhifeng Chen, Craig Citro, Greg S. Corrado, et al. 2016. “TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems.” arXiv Preprint arXiv:1603.04467, March. http://arxiv.org/abs/1603.04467v2.
From the perspective of training pipeline optimization, TPUs simplify integration with data pipelines in the TensorFlow ecosystem. Features such as the TPU runtime and TensorFlow’s tf.data API enable seamless preprocessing, caching, and batching of data to feed the accelerators efficiently (Abadi et al. 2016). Additionally, TPUs are designed to work in pods—clusters of interconnected TPU devices that allow for massive parallelism. In such setups, TPU pods enable hybrid parallelism strategies by combining data parallelism across devices with model parallelism within devices, addressing memory and compute constraints simultaneously.
One of the most notable applications of TPUs is in the training of models like BERT and T5. For instance, Google’s use of TPUs to train BERT demonstrates their ability to handle both the memory-intensive requirements of large transformer models and the synchronization challenges of distributed setups (Devlin et al. 2018). By splitting the model across TPU cores and optimizing communication patterns, Google achieved state-of-the-art results with significantly lower training times compared to traditional hardware.
Devlin, Jacob, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2018. “BERT: Pre-Training of Deep Bidirectional Transformers for Language Understanding,” October, 4171–86. http://arxiv.org/abs/1810.04805v2.
Custom accelerators such as AWS Trainium and Intel Gaudi chips are also gaining traction in the machine learning ecosystem. These devices are designed to compete with TPUs by offering similar performance benefits while catering to diverse cloud and on-premise environments. For example, AWS Trainium provides deep integration with the AWS ecosystem, allowing users to seamlessly scale their training pipelines with services like Amazon SageMaker.
While TPUs and custom accelerators excel in throughput and energy efficiency, their specialized nature introduces limitations. TPUs, for example, are tightly coupled with Google’s ecosystem, making them less accessible to practitioners using alternative frameworks. Similarly, the high upfront investment required for TPU pods may deter smaller organizations or those with limited budgets. Despite these challenges, the performance gains offered by custom accelerators make them a compelling choice for large-scale training tasks.
In summary, TPUs and custom accelerators address many of the key challenges in machine learning training systems, from handling massive datasets to optimizing distributed training. Their unique architectures and deep integration with specific ecosystems make them powerful tools for organizations seeking to scale their training workflows. As machine learning models and datasets continue to grow, these accelerators are likely to play an increasingly central role in shaping the future of AI training.
8.8.3 FPGAs
Field-Programmable Gate Arrays (FPGAs) are versatile hardware solutions that allow developers to tailor their architecture for specific machine learning workloads. Unlike GPUs or TPUs, which are designed with fixed architectures, FPGAs can be reconfigured dynamically, offering a unique level of flexibility. This adaptability makes them particularly valuable for applications that require customized optimizations, low-latency processing, or experimentation with novel algorithms.
Microsoft had been exploring the use of FPGAs for a while, as seen in Figure 8.19, with one prominent example being Project Brainwave. This initiative leverages FPGAs to accelerate machine learning workloads in the Azure cloud. Microsoft chose FPGAs for their ability to provide low-latency inference (not training) while maintaining high throughput. This approach is especially beneficial in scenarios where real-time predictions are critical, such as search engine queries or language translation services. By integrating FPGAs directly into their data center network, Microsoft has achieved significant performance gains while minimizing power consumption.
From a training perspective, FPGAs offer unique advantages in optimizing training pipelines. Their reconfigurability allows them to implement custom dataflow architectures tailored to specific model requirements. For instance, data preprocessing and augmentation steps, which can often become bottlenecks in GPU-based systems, can be offloaded to FPGAs, freeing up GPUs for core training tasks. Additionally, FPGAs can be programmed to perform operations such as sparse matrix multiplications, which are common in recommendation systems and graph-based models but are less efficient on traditional accelerators (Putnam et al. 2014).
Putnam, Andrew, Adrian M. Caulfield, Eric S. Chung, Derek Chiou, Kypros Constantinides, John Demme, Hadi Esmaeilzadeh, et al. 2014. “A Reconfigurable Fabric for Accelerating Large-Scale Datacenter Services.” ACM SIGARCH Computer Architecture News 42 (3): 13–24. https://doi.org/10.1145/2678373.2665678.
In distributed training systems, FPGAs provide fine-grained control over communication patterns. This control allows developers to optimize inter-device communication and memory access, addressing challenges such as parameter synchronization overheads. For example, FPGAs can be configured to implement custom all-reduce algorithms for gradient aggregation, reducing latency compared to general-purpose hardware.
Despite their benefits, FPGAs come with challenges. Programming FPGAs requires expertise in hardware description languages (HDLs) like Verilog or VHDL, which can be a barrier for many machine learning practitioners. To address this, frameworks like Xilinx’s Vitis AI and Intel’s OpenVINO have simplified FPGA programming by providing tools and libraries tailored for AI workloads. However, the learning curve remains steep compared to the well-established ecosystems of GPUs and TPUs.
Microsoft’s use of FPGAs highlights their potential to integrate seamlessly into existing machine learning workflows. By incorporating FPGAs into Azure, Microsoft has demonstrated how these devices can complement other accelerators, optimizing end-to-end pipelines for both training and inference. This hybrid approach leverages the strengths of FPGAs for specific tasks while relying on GPUs or CPUs for others, creating a balanced and efficient system.
In summary, FPGAs offer a compelling solution for machine learning training systems that require customization, low latency, or novel optimizations. While their adoption may be limited by programming complexity, advancements in tooling and real-world implementations like Microsoft’s Project Brainwave demonstrate their growing relevance in the AI hardware ecosystem.
8.8.4 ASICs
Application-Specific Integrated Circuits (ASICs) represent a class of hardware designed for specific tasks, offering unparalleled efficiency and performance by eschewing the general-purpose flexibility of GPUs or FPGAs. Among the most innovative examples of ASICs for machine learning training is the Cerebras Wafer-Scale Engine (WSE), as shown in Figure 8.20, which stands apart for its unique approach to addressing the computational and memory challenges of training massive machine learning models.
The Cerebras WSE is unlike traditional chips in that it is a single wafer-scale processor, spanning the entire silicon wafer rather than being cut into smaller chips. This architecture enables Cerebras to pack 2.6 trillion transistors and 850,000 cores onto a single device. These cores are connected via a high-bandwidth, low-latency interconnect, allowing data to move across the chip without the bottlenecks associated with external communication between discrete GPUs or TPUs (Feldman et al. 2020).
Feldman, Andrew, Sean Lie, Michael James, et al. 2020. “The Cerebras Wafer-Scale Engine: Opportunities and Challenges of Building an Accelerator at Wafer Scale.” IEEE Micro 40 (2): 20–29. https://doi.org/10.1109/MM.2020.2975796.
From a machine learning training perspective, the WSE addresses several critical bottlenecks:
- Data Movement: In traditional distributed systems, significant time is spent transferring data between devices. The WSE eliminates this by keeping all computations and memory on a single wafer, drastically reducing communication overhead.
- Memory Bandwidth: The WSE integrates 40 GB of high-speed on-chip memory directly adjacent to its processing cores. This proximity allows for near-instantaneous access to data, overcoming the latency challenges that GPUs often face when accessing off-chip memory.
- Scalability: While traditional distributed systems rely on complex software frameworks to manage multiple devices, the WSE simplifies scaling by consolidating all resources into one massive chip. This design is particularly well-suited for training large language models and other deep learning architectures that require significant parallelism.
A key example of Cerebras’ impact is its application in natural language processing (NLP). Organizations using the WSE have demonstrated substantial speedups in training transformer models, which are notoriously compute-intensive due to their reliance on attention mechanisms. By leveraging the chip’s massive parallelism and memory bandwidth, training times for models like BERT have been significantly reduced compared to GPU-based systems (Brown, Mann, Ryder, Subbiah, Kaplan, Dhariwal, et al. 2020).
Brown, Tom B., Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, et al. 2020. “Language Models Are Few-Shot Learners.” arXiv Preprint arXiv:2005.14165, May. http://arxiv.org/abs/2005.14165v4.
However, the Cerebras WSE also comes with limitations. Its single-chip design is optimized for specific use cases, such as dense matrix computations in deep learning, but may not be as versatile as multi-purpose hardware like GPUs or FPGAs. Additionally, the cost of acquiring and integrating such a specialized device can be prohibitive for smaller organizations or those with diverse workloads.
Cerebras’ strategy of targeting the largest models aligns with the trends discussed earlier in this chapter, such as the growing emphasis on scaling techniques and hybrid parallelism strategies. The WSE’s unique design addresses challenges like memory bottlenecks and inter-device communication overhead, making it a pioneering solution for next-generation AI workloads.
In conclusion, the Cerebras Wafer-Scale Engine exemplifies how ASICs can push the boundaries of what is possible in machine learning training. By addressing fundamental bottlenecks in computation and data movement, the WSE offers a glimpse into the future of specialized hardware for AI, where the integration of highly optimized, task-specific architectures unlocks unprecedented performance.
8.9 Conclusion
AI training systems are built upon a foundation of mathematical principles, computational strategies, and architectural considerations. The exploration of neural network computation has shown how core operations, activation functions, and optimization algorithms come together to enable efficient model training, while also emphasizing the trade-offs that must be balanced between memory, computation, and performance.
The design of training pipelines incorporates key components such as data flows, forward and backward passes, and memory management. Understanding these elements in conjunction with hardware execution patterns is essential for achieving efficient and scalable training processes. Strategies like parameter updates, prefetching, and gradient accumulation further enhance the effectiveness of training by optimizing resource utilization and reducing computational bottlenecks.
Distributed training systems, including data parallelism, model parallelism, and hybrid approaches, are topics that we examined as solutions for scaling AI training to larger datasets and models. Each approach comes with its own benefits and challenges, highlighting the need for careful consideration of system requirements and resource constraints.
Altogether, the combination of theoretical foundations and practical implementations forms a cohesive framework for addressing the complexities of AI training. By leveraging this knowledge, it is possible to design robust, efficient systems capable of meeting the demands of modern machine learning applications.